2.1 映射与函数
〖考纲要求〗了解映射的概念,在此基础上理解函数及其有关概念.
〖复习要求〗掌握函数的有关概念及三种表示方法,会求简单函数的解析式.
〖复习建议〗在理解映射概念的基础上,深刻理解函数的概念――非空数集之间的映射,函数定义的三要素中,定义域是函数的灵魂,对应法则是核心,要学会用函数的观点与思想解决方程、不等式和数列问题,要理解函数的符号,掌握函数表示法,会判断两个函数是否是同一函数.
〖双基回顾〗1、A到B的映射: ;
2、集合A中有n个元素,集合B中有m个元素,那么从A到B的映射有 个;
3、函数的近代定义是: ;
4、函数的三要素是: ;
〖重点难点〗函数表达式的建立
一、知识点训练:
1、下列是映射的是…………………………………………………………………………………( )

(A)1、2、3 (B)1、2、5 (C)1、3、5 (D)1、2、3、5
2、设集合A={a,b,c},B={0,1},那么从B到A的映射有………………………………( )
(A)3个 (B)6个 (C)8个 (D)9个
3、下列与函数y=x是同一函数的是……………………………………………………………( )
(A)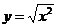 (B)
(B)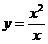 (C)
(C)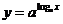 (D)
(D)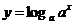
4、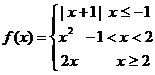 ,那么f(f(-2))= ;如果f(a)=3,那么实数a=
.
,那么f(f(-2))= ;如果f(a)=3,那么实数a=
.
二、典型例题分析:
1、已知 =2x-1,
=2x-1,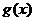 =
=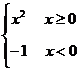 ,求f(g(x))和g(f(x))的表达式.
,求f(g(x))和g(f(x))的表达式.
2、A、B两地相距150km,某汽车以50km/h的速度从A到B,到达B后在B地停留2个小时之后又从B地以60km/h的速度返回,写出该车离开A地的距离S(km)与时间t(小时)的函数关系.
3、求满足下列条件的函数解析式:
⑴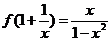 ⑵
⑵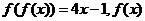 是一次函数.
是一次函数.
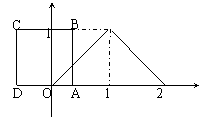
4、如图,把边长为1的正方形沿x正方向平移,设OA=x,把此正方形与图中的三角形的公共部分的面积S表示为x的函数.
 |
三、课堂练习:
1、映射 ,其中A={-3,-2,-1,1,2,3,4},集合B中的元素都A中的元素在映射f下的象,且对于任意的a∈A,在集合B中和它对应的元素是|a|,则B中的元素有……( )
,其中A={-3,-2,-1,1,2,3,4},集合B中的元素都A中的元素在映射f下的象,且对于任意的a∈A,在集合B中和它对应的元素是|a|,则B中的元素有……( )
(A)4个 (B)5个 (C)6个 (D)7个
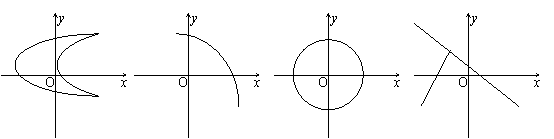 2、下面哪一个图形可以作为函数的图象…………………………………………………………( )
2、下面哪一个图形可以作为函数的图象…………………………………………………………( )
 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
3、如图为函数y= 的图象,
的图象,
那么此函数的表达式为 .
四、课堂小结:
1、映射概念的理解应从以下几个方面进行:A、B非空;A中无剩余;单值对应.
2、理解函数与映射的关系要注意:函数是特殊的映射即有“f是函数”是“f是映射”的充分不必要条件.
3、在书写分段函数的表达式时,要注意定义域的合理性.
4、具有实际意义的函数的定义域必须具有实际意义.
五、能力测试: 姓名 得分
1、M={3,4,5},N={-1,0,1},从M到N的映射f满足x+f(x)是偶数,这样的映射有( )
(A)3 (B) 4 (C)27 (D) 9
2、如果(x,y)在映射f下的象为(x+y,x-y),那么(1,2)的原象是……………………( )
(A)(-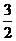 ,
,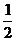 ) (B) (
) (B) (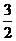 ,-
,-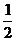 ) (C) (-
) (C) (-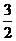 ,-
,-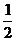 ) (D) (
) (D) (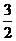 ,
,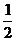 )
)
3、函数f(x)=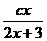 ,满足
,满足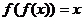 恒成立,那么常数c的值是………………………( )
恒成立,那么常数c的值是………………………( )
(A)3 (B) -3 (C)3或者-3 (D) 8或者-3
4、下列各组函数中,f(x)与g(x)相同的是…………………………………………………( )
(A)f(x)=lnx , g(x)= (B)f(x)=x,g(x)=
(B)f(x)=x,g(x)=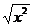
(C) ,g(x)=f-1(x) (D) f(x)=0.1lg(2x-1),
,g(x)=f-1(x) (D) f(x)=0.1lg(2x-1),
5、已知f(x)是表示经过(0,-2)的一条直线,g(x)表示经过(0,0)的另一直线,如果又有关系f(g(x))=g(f(x))=3x-2,求这两条直线的交点坐标.
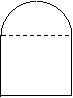
6、用长为l的铁丝弯成下部为矩形,上部为半圆的框架,如果设底边长为2x, 求此框架围成的面积y与x的函数关系式,并且求出其定义域及面积最大值.
7、建造一个容积为2000m3,深为5m的长方体水池,池底每平方米的造价100元,池壁每平方米造价75元,设总造价为y元,底面一边长为x米,求y关于x的函数解析式及其定义域及值域.
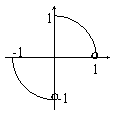
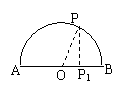 8、AB是单位半圆的直径,动点P从A出发先过半圆弧再沿BA回到A点,试把动点P到点A的水平距离S表示为路程x的函数.
8、AB是单位半圆的直径,动点P从A出发先过半圆弧再沿BA回到A点,试把动点P到点A的水平距离S表示为路程x的函数.
2.2 函数的定义域与值域
〖考纲要求〗理解函数的定义域,理解函数的值域与最值的概念,会求简单函数的值域与最值
〖复习要求〗理解函数定义域意义,会求有关函数的定义域,掌握求简单函数的值域与最值的方法
〖复习建议〗由所给函数表达式会求其定义域;会求复合函数的定义域;会根据函数的定义域情况讨论函数表达式中参数的取值范围;掌握有实数意义的函数定义域的求法.
求函数的值域主要从以下几个方法入手:观察法、配方法、判别式法、单调性法、不等式法、部分分式法、换元法、有界性法、数形结合法,其中最为重要的是:观察法、判别式法、单调性法、不等式法、有界性法、数形结合法.
〖双基回顾〗⑴一次函数与二次函数、正余弦函数的定义域
⑵无理函数与对数函数、正余切函数的定义域
⑶分式函数与最简单的幂函数的定义域
⑷一般复合函数的定义域的求法.
⑸反函数的定义域与原函数的值域的关系.
特别提示:函数的定义域不可能是空集.
一、知识点训练:
1、函数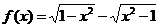 的定义域为…………………………………………………( )
的定义域为…………………………………………………( )
(A)空集 (B)单元素集 (C)无限集 (D)双元素集
2、如果函数f(x)的定义域为[0,2],那么函数f(x+3)的定义域为……………………………( )
(A)[3,5] (B)[0,2] (C)[-3,0] (D)[-3,-1]
3、函数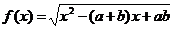 的定义域为M,函数
的定义域为M,函数 的定义域为N(a>b>0),则下列关系正确的是……………………………………………………………( )
的定义域为N(a>b>0),则下列关系正确的是……………………………………………………………( )
(A)M N (B)M
N (B)M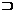 N
(C)M
N
(C)M N=
N=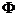 (D)M=N
(D)M=N
4、下列函数值域为R+的是…………………………………………………………………………( )
(A) (B )
(B ) (C)
(C)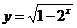 (D)y=x2+x+1
(D)y=x2+x+1
5、函数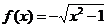 (x≤-2)的反函数的定义域为………………………………………( )
(x≤-2)的反函数的定义域为………………………………………( )
(A)  (B )
(B ) 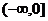 (C)
(C) (D)
(D)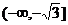
6、函数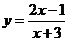 的值域为
;7、函数
的值域为
;7、函数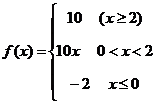 的值域为
.
的值域为
.
二、典型例题分析:
1、 求下列函数的定义域:
⑴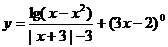 ;
⑵
;
⑵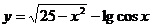 ;
;
⑶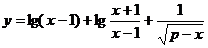 .
.
2、已知扇形周长为10,求此扇形的面积S与半径r之间的函数关系式并且求其定义域.
3、如果函数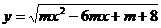 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
4、⑴求值域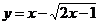 ⑵求值域
⑵求值域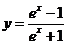 ⑶求值域y
⑶求值域y .
.
⑷函数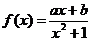 的值域为[-1,4],求实数a、b的值
的值域为[-1,4],求实数a、b的值
三、课堂练习:
1、 的定义域为A,
的定义域为A, 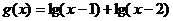 的定义域为B,则…( )
的定义域为B,则…( )
(A)A=B (B)A∩B=φ (C)A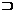 B
(D)A
B
(D)A B
B
2、如果函数f(x)的定义域为[-1,3],那么函数f(x)-f(-x)的定义域为 .
3、如果函数f(x)=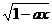 的定义域为[-
的定义域为[-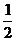 ,+
,+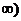 ,那么实数a的取值范围是
.
,那么实数a的取值范围是
.
5、函数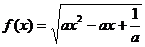 的定义域为R,那么实数a的取值范围是
.
的定义域为R,那么实数a的取值范围是
.
6、用适当的方法求下列函数的值域:
⑴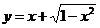 (换元法)
⑵
(换元法)
⑵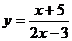 (部分分式法)
(部分分式法)
四、能力测试: 姓名 得分
1、函数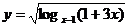 的定义域是……………………………………………………………( )
的定义域是……………………………………………………………( )
(A)(2,+∞)
(B) (1,2)∪(2,+∞) (C) (1,+∞) (D)(-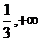 )
)
2、函数 的定义域为R,那么实数a的取值范围是………………………( )
的定义域为R,那么实数a的取值范围是………………………( )
(A)(-∞,+∞)
(B)(0,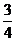 ) (C) (-
) (C) (-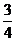 ,+∞) (D)
,+∞) (D)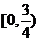
3、如果函数 的图象在x轴上方,那么此函数的定义域为……………( )
的图象在x轴上方,那么此函数的定义域为……………( )
(A)(-1,1) (B)(1,+∞)∪(-∞,-1) (C)(-∞,1)且x≠-1 (D)(-1,+∞)且x≠1
4、函数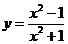 的值域为…………………………………………………………………………( )
的值域为…………………………………………………………………………( )
(A)(-1,1)
(B)[+1,1] (C)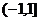 (D)
(D)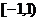
5、函数f(x)的值域为[-2,2],则函数f(x+1)的值域为……………………………………( )
(A)[-1,3] (B)[-3,1] (C)[-2,2] (D)[-1,1]
6、函数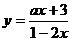 的值域为(-∞,-2)∪(-2,+∞),则实数a=
.
的值域为(-∞,-2)∪(-2,+∞),则实数a=
.
7、函数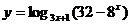 的定义域为
.
的定义域为
.
8、函数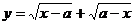 的定义域为
.
的定义域为
.
9、函数 =x2+x+
=x2+x+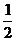 的定义域是[n,n+1](n是自然数),则此函数值域中的整数一共有 个.
的定义域是[n,n+1](n是自然数),则此函数值域中的整数一共有 个.
10、如果函数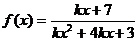 的定义域为R,则实数k的取值范围是
.
的定义域为R,则实数k的取值范围是
.
11、求函数 的值域
的值域
12、求函数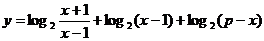 的定义域和值域.
的定义域和值域.
2.3 函数的单调性
〖考纲要求〗理解增函数、减函数的定义,并会运用定义判定或证明一些简单函数的增减性;能结合函数的图象划分函数的单调区间;
〖复习要求〗理解增函数、减函数的定义,并会运用定义判定或证明一些简单函数的增减性;能结合函数的图象划分函数的单调区间;会讨论复合函数的单调性.
〖复习建议〗理解增函数、减函数的定义,掌握判断函数单调性的方法与步骤:设值、作差、比较、结论,能借助图象寻找函数的单调区间,掌握简单的复合函数单调性规律,学会用变量变化规律逐步寻找函数变化规律的判断方法
〖双基回顾〗1、函数y=f(x)在其定义域的一个子区间M上为增函数(减函数)的充要条件是:
、在此区间M上,函数的图象是 ;如果函数y=f(x)在区间M上为增函数或为减函数,则称在M上具有 、M称为f(x)的 .
2、一次函数y=kx+b,当k>0时,在 上是 函数、当k<0时,在 上是 函数、
3、奇函数y=f(x)在区间[a,b]上是减函数,那么它在区间[-b,-a]上是 ;偶函数y=f(x)在区间[a,b]上是减函数,那么它在区间[-b,-a]上是 .(填增减性)
4、函数y=x+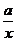 (a>0)的单调区间为
.(记住这个结论)
(a>0)的单调区间为
.(记住这个结论)
一、基础知识练习:
1、奇函数f(x)在[3,7]上单调递增且最小值为5,那么在[-7,-3]上……………………( )
(A)递增,最小-5 (B)递减,最小-5 (C)递增,最大-5 (D)递减,最大-5
2、函数f(x)在[a,b]上单调并且f(a)?f(b)<0,则方程f(x)=0在[a,b]上…………( )
(A)至少一解 (B)至多一解 (C)恰一解 (D)无解
3、函数f(x)=x2+mx+n满足f(2+t)=f(2-t),那么a=f(1),b=f(2),c=f(4)的大小关系是…………( )
(A)b<a<c (B)a<b<c (C) b<c<a (D) c<b<a
4、函数y=(2k+1)x+b在R上为减函数,则k∈ .
5、f(x)=loga|x+1|在(-1,0)上恒正,则在(-∞,-1)上f(x)=loga|x+1|的单调性为 .
6、函数f(x)=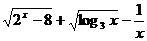 的值域为
.
的值域为
.
二、典型例题分析:
1、x>0时 <0,并且
<0,并且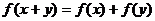 ,求证:y=
,求证:y= 是减函数
是减函数
2、求下列函数的单调区间:
⑴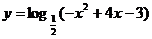 ⑵y=lg(3sin(-x))
⑵y=lg(3sin(-x))
3、函数 =
=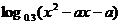 在
在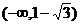 上递增,求实数a的取值范围.
上递增,求实数a的取值范围.
4、判断函数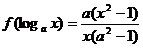 的单调性.
的单调性.
5、是否存在实常数k,使 =
=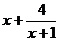 在(0,k)上递减,而在(k,+∞)上递增?
在(0,k)上递减,而在(k,+∞)上递增?
6、定义在[-1,1]上的函数y=f(x)是减函数,且是奇函数,若f(a2-a-1)+f(4a-5)>0,求实数a的取值范围.
三、课堂练习:
1、在区间(0,2)上是增函数的是……………………………………………………………………( )
(A)y=-x+1 (B)y=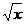 (C)y= x2-4x+5 (D)y=
(C)y= x2-4x+5 (D)y=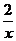
2、函数y=f(x)是单调函数,则方程f(x)=a…………………………………………………………( )
(A)至少一个解 (B)至多一个解 (C)恰一个解 (D)无穷多个解
3、函数 y=f(x)在A上是增函数,在B上也是增函数,则在A∪B上的单调性为……………( )
(A)增函数 (B)减函数 (C)不确定 (D)先增后减
4、函数f(x)=x2+px+3在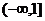 上单调递减,在
上单调递减,在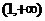 上单调递增,则p= .
上单调递增,则p= .
5、函数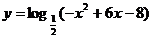 的单调递减区间为
.
的单调递减区间为
.
四、能力测试: 姓名 得分
1、下列函数中,在区间(-∞,0)上是增函数的是……………………………………………………( )
(A)y=x2-4x+8 (B)y=ax+3(a≥0) (C)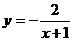 (D)
(D)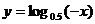
2、函数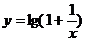 在区间(0,+∞)上是…………………………………………………………( )
在区间(0,+∞)上是…………………………………………………………( )
(A)正值增函数 (B)负值减函数 (C)正值减函数 (D)负值减函数
3、偶函数y=loga|x-b|在(-∞,0)上递增,则a、b满足…………………………………………( )
(A)0<a<1,b=0 (B)a>1,b∈R (C)a>1,b>0 (D)a>1,b=0
4、如果函数y= 是R上的奇函数又是减函数,那么函数
是R上的奇函数又是减函数,那么函数 是………………………( )
是………………………( )
(A)减函数、奇函数 (B)增函数、奇函数 (C)减函数、偶函数 (D)增函数、偶函数
5、如果函数f(x)=x2+2(a-1)x+2在区间(-¥,4]上是减函数,则a的取值范围是 ;
6、函数y=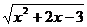 的递减区间为
.
的递减区间为
.
7、已知函数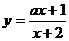 在区间(-2,+∞)上是增函数,试求a的取值范围.
在区间(-2,+∞)上是增函数,试求a的取值范围.
8、y= 是[-1,1]上的减函数,又是奇函数.
是[-1,1]上的减函数,又是奇函数.
⑴求证: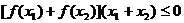 (提示:可分x1+x2≥0与x1+x2≤0证明)
(提示:可分x1+x2≥0与x1+x2≤0证明)
⑵解不等式: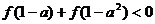
*9、 =
=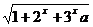 在(-∞,1)有意义,求实数a的取值范围
在(-∞,1)有意义,求实数a的取值范围
2.4 函数的奇偶性
〖考纲要求〗理解函数的奇偶性的概念,并能判定一些简单函数的奇偶性;理解奇函数和偶函数的图象的对称性,并能用对称性描绘奇函数或偶函数的图象.
〖复习要求〗会判断函数的奇偶性,能利用函数的奇偶性解决一些实际问题.
〖复习建议〗要正确理解函数的奇偶性的定义,奇偶函数的定义是判定函数奇偶性的根本依据,但要注意:
1、函数为奇函数或偶函数的必要条件是其定义域为关于原点对称的区间;
2、f(-x)=-f(x)Û f(-x)+f(x)=0Û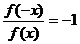 ( f(x)≠0)、
( f(x)≠0)、
f(-x)=f(x)Û f(-x)-f(x)=0Û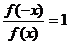 ( f(x)≠0);
( f(x)≠0);
3、奇偶性:奇函数、偶函数、又奇又偶、非奇非偶,要学会用图象判断函数的奇偶性
〖双基回顾〗
1、若函数f(x)为定义域为D的奇函数,则f(x)应满足:⑴对任意x∈D,都有 ;(或者说函数f(x)的定义域是 的区间)⑵f(-x)= ;若函数f(x)为定义域为D的偶函数,则f(x)应满足:⑴对任意x∈D,都有 ;⑵f(-x)= ;
2、奇函数的图象关于 对称;偶函数的图象关于 对称.
3、若非零函数f(x)、g(x)的奇偶性相同,则在公共定义域内,H(x)=f(x)g(x)为 ;若非零函数f(x)、g(x)的奇偶性相反,则在公共定义域内,H(x)=f(x)g(x)为 .
4、若f(x)的定义域为R,且当x∈[0,+¥)时为增函数,则当f(x)为奇函数时,它在(-¥,0)上为_____
、当f(x)为偶函数时,它在(-¥,0)上为 .(填奇偶性)
1、判断下列函数的奇偶性:
一、典型例题分析:
⑴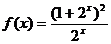 ;
⑵f(x)=
;
⑵f(x)=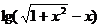 ;
⑶
;
⑶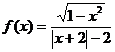 ;
;
⑷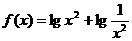 ;
⑸
;
⑸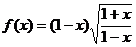
2、如果函数f(x)满足:f(x+y)+ f(x-y)=2 f(x) f(y),f(0)≠0,判定函数f(x)的奇偶性.
3、奇函数f(x)的定义域是R,当x>0时,f(x)=-x2+2x+2,求f(x)在R上的表达式,并作出的图象.
4、已知f(x)=(m2-1)x2+(m-1)x+n+2为奇函数,求m、n.
5、已知.f(x)=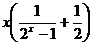 ,⑴判断f(x)的奇偶性;⑵证明f(x)>0.
,⑴判断f(x)的奇偶性;⑵证明f(x)>0.
二、课堂练习:
1、函数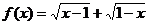 的奇偶性是………………………………………………………( )
的奇偶性是………………………………………………………( )
(A)奇函数 (B)偶函数 (C)既奇又偶函数 (D)非奇非偶函数
2、已知y=f(x)(x∈R)是奇函数,则下列各点中,在曲线y=f(x)上的点是…………………………( )
(A)(a,f(-a)) (B)(-sina,-f(-sina)) (C)(-lga, -f(lg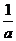 )) (D)(-a,-f(a))
)) (D)(-a,-f(a))
3、既奇又偶函数的函数的个数为……………………………………………………………………( )
(A)一个 (B)二个 (C)无穷多 (D)不存在
4、偶函数y=f(x)在x≥0时,f(x)=sin2x-2sinx,则x<0时,f(x)= .
三、课堂小结:
1、 函数的奇偶性是函数在整个定义域上的性质,前提条件是:定义域关于原点对称,所以在判断函数奇偶性时,首先必须求函数的定义域.
2、 复杂函数奇偶性的判定可以改判定方式为:判断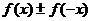 是否等于0.
是否等于0.
3、函数奇偶性应用是一个重要的内容,千万不能忽视.
四、能力测试: 姓名 得分
1、函数y=x(|x|-1)(|x|≤3)的奇偶性是…………………………………………………………( )
(A)奇函数 (B)偶函数 (C)非奇非偶函数 (D)既奇又偶函数
2、定义在R上的函数f(x)满足:f(x+y) =f(x)- f(y),那么此函数是……………………………( )
(A)奇函数 (B)偶函数 (C)非奇非偶函数 (D)既奇又偶函数
3、已知y=f(x)是定义在R上的奇函数,当x≥0时f(x)=x2-2x,则在R上,f(x)的解析式是…( )
(A)x(x-2) (B)x[|x|-2] (C)|x|(x-2) (D)|x|[|x|-2]
4、已知f(x)=x5+ax3+bx-8,且f(-2)=10,那么f(2)等于………………………………………( )
(A)-26 (B)-18 (C)-10 (D)10
5、已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则a= 、b= .
6、判断下列函数的奇偶性:
(1)f(x)=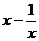 ;
(2)
;
(2)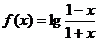 ;
;
7、如果函数y=f(x)是偶函数,y=g(x)是奇函数,且f(x)+g(x)=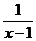 ,求f(x)与、g(x)的表达式.
,求f(x)与、g(x)的表达式.
(求证:函数y=f(x)的定义域关于原点对称,则y=f(x)一定可以表示为一个奇函数和一个偶函数之和)
8、奇函数y=f(x)满足x<0时,f(x)=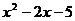 ,求函数y=f(x)的表达式并且解方程f(x)=2x.
,求函数y=f(x)的表达式并且解方程f(x)=2x.
9、已知f(x)= ,如果 xg(x)>0,求证:f(x)>0.
,如果 xg(x)>0,求证:f(x)>0.
2.5 反函数
〖考纲要求〗掌握互相为反函数图象之间的关系.
〖复习要求〗理解反函数的概念,知道什么函数有反函数,会求一个函数的反函数,掌握互为反函数图象之间的关系.
〖复习建议〗记住求反函数的步骤,知道原函数与反函数的定义域、值域关系,图象关系,单调性关系,能利用反函数研究原函数的性质.
〖双基回顾〗
1、求反函数的三个步骤是:⑴ ⑵ ⑶ .
2、原函数的定义域是反函数的 ;原函数的值域是反函数的 .
3、原函数的图象与反函数的图象关于 .
4、原函数与反函数具有 单调性.
5、函数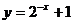 的反函数为…………………………………………………………………( )
的反函数为…………………………………………………………………( )
(A)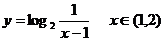 (B)
(B) 
(C) 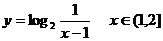 (D)
(D) 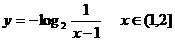
6、判断:原函数与反函数图象的交点一定在直线y=x上,对吗?
一、典型例题分析:
1、求下列函数的反函数:
⑴ 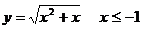 ⑵
⑵ 
2、函数 ,则实数a、b为何值时,
,则实数a、b为何值时, .
.
3、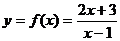 ,
,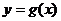 的图象与
的图象与 的图象关于直线y=x对称,求
的图象关于直线y=x对称,求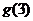 的值.
的值.
4、设0<a≠1,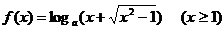
⑴求函数 的反函数
的反函数
⑵如果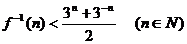 ,求实数a的取值范围.
,求实数a的取值范围.
二、课堂练习:
1、下列哪一组的两个函数是互为反函数 …………………………………………………………( )
(A) f(x)=tgx,g(x)=ctgx (B) f(x)=lgx,g(x)=ex
(C) f(x)=x2 ,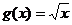 (D)
(D) 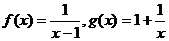
2、已知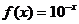 ,那么
,那么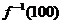 =……………………………………………………………( )
=……………………………………………………………( )
(A) -2 (B)
-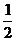 (C)
(C) 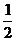 (D)
2
(D)
2
3、已知f(x)=3x-2,则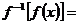 .
.
4、函数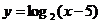 的反函数是
.
的反函数是
.
三、课堂小结:
1、反函数的定义域不能由其解析式确定,应该是原函数的定义域.
2、互为反函数的两个函数的图象具有相同的增减性,他们的图象关于直线y=x对称.
3、分段函数的反函数,应该分别求出各段的反函数,再合成.
四、能力测试: 姓名 得分
1、函数y=x2在下列区间不存在反函数的是………………………………………………………… ( )
(A) (B)
(B) 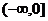 (C)
[-1,1]
(D) [0,1]
(C)
[-1,1]
(D) [0,1]
2、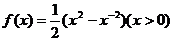 ,则
,则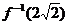 =…………………………………………………( )
=…………………………………………………( )
(A)3+2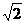 (B) 3-2
(B) 3-2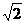 (C) 1+
(C) 1+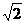 (D)
1-
(D)
1-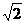
3、如果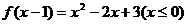 ,则
,则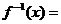 ……………………………………………( )
……………………………………………( )
(A)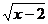 x≥2 (B) -
x≥2 (B) -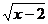 x≥2 (C)
-
x≥2 (C)
-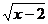 x≥3 (D)
x≥3 (D) 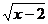 x≥3
x≥3
4、函数y=2x-1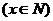 的反函数是 ……………………………………………………………… ( )
的反函数是 ……………………………………………………………… ( )
(A) 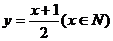 (B)
(B) 
(C) 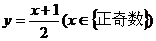 (D)
(D) 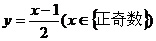
5、函数y= 的反函数为y=
的反函数为y=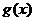 ,具有
,具有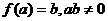 ,则
,则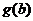 =……………………( )
=……………………( )
(A)a
(B)b
(C)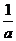 (D)
(D) 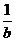
6、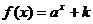 的图象过点A(1,3),函数
的图象过点A(1,3),函数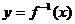 的图象过点B(2,0),则f(x)的表达式为
.
的图象过点B(2,0),则f(x)的表达式为
.
7、f-1(x)=log3(2x-1),则f(3)= .
8、⑴求函数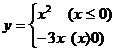 的反函数
的反函数
⑵若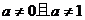 ,求证:函数
,求证:函数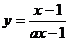 的图象关于直线y=x对称
的图象关于直线y=x对称
*9、设函数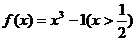 的图象为C1,C1关于直线y=x的对称图象为C2.
的图象为C1,C1关于直线y=x的对称图象为C2.
⑴求C2对应的函数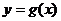 的解析式及定义域M
的解析式及定义域M
⑵对任意x1、x2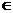 M,并且x1≠x2,求证:
M,并且x1≠x2,求证: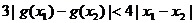
2.6 指数、对数函数
 〖考纲要求〗掌握指数函数与对数函数的概念、图象、性质
〖考纲要求〗掌握指数函数与对数函数的概念、图象、性质
〖复习建议〗掌握指数函数与对数函数的概念以及相互间的关系,熟悉它们的图象,牢记主要的性质,会对这两种函数的底数分大于1和在(0,1)之间进行讨论,注意对数函数的真数要求,掌握几个数的大小比较方法.
〖双基回顾〗(见右表,注意指数函数与对数
函数是一对反函数)
〖知识点训练〗
1、已知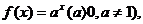 当
当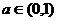
时 (增函数,减函数);
(增函数,减函数);
当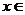 ,
, .
.
2、已知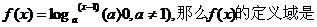 ;
;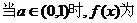
(增函数,减函数);当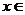 时,f(x)<0.
时,f(x)<0.
3、当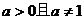 时,函数
时,函数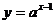 +3的图象一定经过点
;函数
+3的图象一定经过点
;函数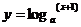 的反函数图象一定经过点
.
的反函数图象一定经过点
.
4、已知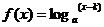 的图象经过点(4,0),而且其反函数
的图象经过点(4,0),而且其反函数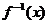 的图象过点(1,7),则f(x)是 …( )
的图象过点(1,7),则f(x)是 …( )
(A)增函数 (B) 减函数 (C) 奇函数 (D) 偶函数
5、函数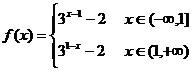 的值域为
.
的值域为
.
6、不等式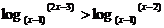 的一个充分但不必要条件是……………………………… ( )
的一个充分但不必要条件是……………………………… ( )
(A)x>2 (B) x>4 (C) 1<x<2 (D) x>1
一、典型例题分析:
1、 (1)如果0<a<b<1,试比较ab与ba的大小.
(2)如果0<a<1, b=aa,c=ab,试比较a、b、c的大小关系.
2、函数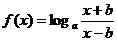 (0<a≠1,b>0)
(0<a≠1,b>0)
⑴求此函数的定义域; ⑵判断此函数的奇偶性;
⑶判断此函数的单调性; ⑷求此函数的反函数;
3、设函数 =
= ,其中a是实数,如果当x∈
,其中a是实数,如果当x∈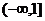 时,
时, 有意义,求实数a 的取值范围.
有意义,求实数a 的取值范围.
4、已知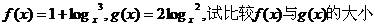
二、课堂练习:
1、已知0<a<1,必有………………………………………………………………………………( )
(A)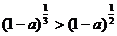 (B)
(B)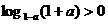 (C)(1-a)3>(1-a)2 (D)(1-a)1+a>1
(C)(1-a)3>(1-a)2 (D)(1-a)1+a>1
2、镭经过100年剩余原来质量的95.76%,设质量为1的镭经过x年剩余量为y,那么y关于x的
函数解析式为 .
3、函数y=3-5x的值域为 .
4、定义在区间(-1,0)上的函数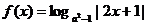 满足:
满足: >0,那么实数a的取值范
>0,那么实数a的取值范
围是………………………………………………………………………………………………( )
(A)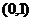 (B)
(B) 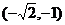
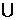
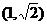 (C)
(C) 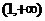 (D)
(D) 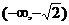
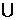
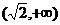
5、设函数 =|lgx|,如果0<a<b<c,
=|lgx|,如果0<a<b<c,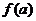 >
> >
>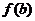 则……………………………( )
则……………………………( )
(A)(c-1)(a-1)>0 (B)ac>1 (C)(a+1)(c+1)<0 (D)ac<1
三、能力测试: 姓名 得分
1、函数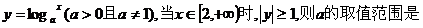 ………………… ( )
………………… ( )
(A)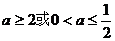 (B)
(B)
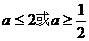 (C)
(C)
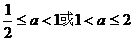 (D)
(D) 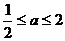
2、若函数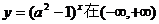 上为减函数,则a的取值范围是……………………………… ( )
上为减函数,则a的取值范围是……………………………… ( )
(A)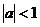 (B)
(B) 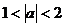 (C)
(C)
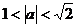 (D)
(D) 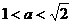
3、函数y=ax-b-1,当a>1,b>0时的图象经过的象限是…………………………………………( )
(A) Ⅰ、Ⅱ、Ⅲ (B)Ⅱ、Ⅲ、Ⅳ (C)Ⅰ、Ⅲ、Ⅳ (D)Ⅰ、Ⅱ、Ⅳ
4、若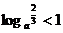 ,则a的取值范围是……………………………………………………………………
( )
,则a的取值范围是……………………………………………………………………
( )
 (A)
(A) (B)
(B)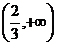 (C)
(C)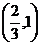 (D)
(D)
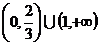
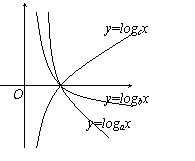
5、图中曲线是三条对数函数的图象,如果a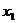 =b
=b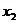 =c
=c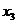 >1,则x1、
>1,则x1、
x2、x3满足………………………………………………………( )
(A) x1>x2>x3 (B) x3>x2>x1
(C) x3>x1>x2 (D) x2>x1>x3
6、已知函数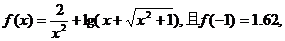 则
则
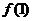 ………………………………………………………………( )
………………………………………………………………( )
(A)0.38 (B)1.62 (C)2.38 (D) 2.62
7、已知函数f(x)的定义域是[0,1],则函数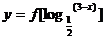 的定义域是 .
的定义域是 .
8、函数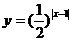 单调递增区间是 .
单调递增区间是 .
9、已知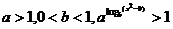 ,则实数x的取值范围是
.
,则实数x的取值范围是
.
10、 =
=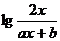 ,
,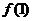 =0,且对x>0时,恒有
=0,且对x>0时,恒有
⑴求实数a、b的值并且求其定义域
⑵求函数的单调区间.
11、已知函数 =
=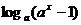 (0<a≠1
(0<a≠1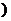
⑴求此函数 的定义域;⑵讨论函数
的定义域;⑵讨论函数 的单调性;⑶解不等式
的单调性;⑶解不等式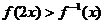 ;
;
2.7 二次问题
〖考纲要求〗理解二次函数的概念,掌握它的图象和性质,能灵活运用二次函数的最值,了解二次函数、一元二次不等式、一元二次方程三者的关系.
〖复习要求〗理解二次函数的概念,掌握它的图象和性质,能灵活运用二次函数的最值以及二次函数的图象和一元二次方程的实根分布范围等知识解决有关问题.了解二次函数、一元二次不等式、一元二次方程三者的关系. 学会把一元二次方程的根的条件转化为图象条件,然后再转化为代数条件,会求含参数的二次函数的最值问题
〖复习建议〗二次函数的关键是通过配方得出顶点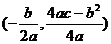 ,由此可知函数的对称性、图象、单调区间、最值和判别式等.
,由此可知函数的对称性、图象、单调区间、最值和判别式等.
二次函数解析式的基本形式有:
⑴标准式: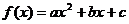 ; ⑵顶点式:
; ⑵顶点式:
⑶零点式:
二次方程的韦达定理很重要
一、知识点训练:
1、函数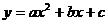 的图象与x轴有交点的充要条件是 ……………………………………( )
的图象与x轴有交点的充要条件是 ……………………………………( )
(A)a=0且b≠0 (B)a≠0 (C)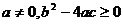 (D)
(D) 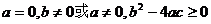
2、已知函数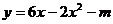 的值恒小于零,那么………………………………………………… ( )
的值恒小于零,那么………………………………………………… ( )
(A)m=9 (B) 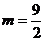 (C)
(C)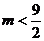 (D)
m
(D)
m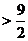
3、二次函数y=ax2+bx+c的图象开口向下,对称轴为x=1,图象与x轴有两个不同的交点,一个交点的横坐标x1∈(2,3),那么………………………………………………………………………( )
(A)ab>0 (B)a+b+c<0 (C)a+c>b (D)3b>2c
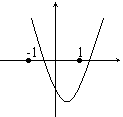 4、二次函数
4、二次函数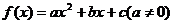 的图象如右图
的图象如右图
试确定下列各式的正负:a ;b ;c ;
a-b+c ;b2-4ac ;a+b+c ;
5、方程x2+(2m-1)x+4-2m=0的一根大于2、一根小于2,那么实数m的取值范围是 .
一、典型例题分析:
1、关于x的方程:3x2-5x+a=0的一根在(-2,0)内,另一根在(1,3)内,求实数k的取值范围.
2、设二次函数f(x)满足f(x-2)=f(-x-2),且图象在y轴上的截距为1,在x轴上截得的线段长为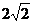 ,求f(x)的表达式
,求f(x)的表达式
3、函数 =x2-2x+2在区间[t,t+1]上的最小值为
=x2-2x+2在区间[t,t+1]上的最小值为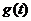 ,求
,求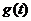 的表达式及其最值.
的表达式及其最值.
4、设f(x)是R上以2为周期的函数,当 时,f(x)=x2,
时,f(x)=x2,
⑴求f(x)在[1,3]上的解析式;⑵求f(-3)、f(3.5);⑶求f(x)的表达式.
5、设x=m时,二次函数f(x)有最大值5;又二次函数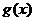 的最小值为-2,
的最小值为-2,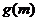 =25,并且f(x)+
=25,并且f(x)+ 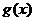 =x2+16x+13(m>0).⑴求实数m的值. ⑵求函数
=x2+16x+13(m>0).⑴求实数m的值. ⑵求函数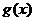 的表达式.
的表达式.
二、课堂练习:
1、f(x)=x2lga-2x+1的图象与x轴有两个不同的交点,那么实数a的取值范围是 .
2、-4<k<0是函数y=kx2-kx-1恒负的 条件.
3、若二次函数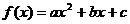 对任意实数x都有f(1+x)=f(1-x),且f(1)<f(2),则
对任意实数x都有f(1+x)=f(1-x),且f(1)<f(2),则 的大小关系为
.
的大小关系为
.
四、能力测试: 姓名 得分
1、函数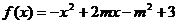 的图象的对称轴为x+2=0,则m= ;顶点坐标为 ;递增区间为
; 递减区间为
.
的图象的对称轴为x+2=0,则m= ;顶点坐标为 ;递增区间为
; 递减区间为
.
2、已知不等式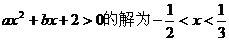 ,则a= ;b= .
,则a= ;b= .
3、函数 =4x2-mx+5在区间
=4x2-mx+5在区间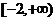 上是增函数,则
上是增函数,则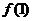 的取值范围是
.
的取值范围是
.
4、二次函数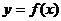 满足
满足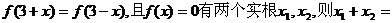 (
)
(
)
(A)0 (B) 3 (C) 6 (D) 不能确定
5、已知函数 上单调递增,则a的取值范围是…………………… ( )
上单调递增,则a的取值范围是…………………… ( )
(A)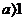 (B)
(B) 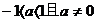 (C)
(C) 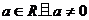 (D)
(D) 
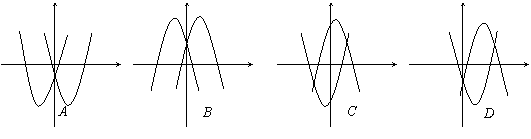 6、两个二次函数
6、两个二次函数 =ax2+bx+c与
=ax2+bx+c与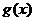 =bx2+ax+c的图象只能是…………………………( )
=bx2+ax+c的图象只能是…………………………( )
7、二次函数f(x)满足:f(x)+ f(x-1)=-2x2+6x+3,求此函数的解析式.(设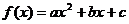 )
)
8、函数 =-x2+2ax+1-a在区间[0,1]上的最大值为2,求实数a的值.
=-x2+2ax+1-a在区间[0,1]上的最大值为2,求实数a的值.
9、x1、x2是方程:(a2+1)x2-2ax-1=0的根满足:x2<x1<1并且x1>|x2|(1-x1),确定实数a的取值范围.
2.8 抽象函数
〖考纲要求〗理解函数及其有关概念.
〖复习要求〗掌握函数的有关概念,会求简单函数的解析式,掌握函数解析式的一些形式变换,理解抽象函数的关系式的意义.
〖复习建议〗掌握一次、二次函数解析式,会用待定系数法求之,会用适当的方法研究抽象函数.
〖双基回顾〗求函数解析式的方法有:直接法、待定系数法、解方程组法、换元法、归纳猜想法…….
一、知识点训练:
1、f(x+1)=2x+1,则f(x)= .
2、如果函数f(x)满足:f(x+y)=f(x)?f(y),f(x)恒不为0,那么f(0)= .
3、f(x)=2x+3,g(x+2)=f(x),则g(x)=………………………………………………………………( )
(A)2x+1 (B)2x-1 (C)2x-3 (D)2x+7
二、典型例题分析:
1、 ⑴如果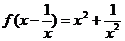 ,求函数f(x)的表达式.
,求函数f(x)的表达式.
⑵如果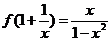 ,求函数f(x)的表达式.
,求函数f(x)的表达式.
2、二次函数y=f(x)满足:f(x)=f(2-x)并且x>1时f(x)为增函数,如果a=f(0),b=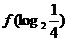 ,c=
,c=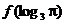 ,试比较a、b、c的大小
,试比较a、b、c的大小
3、对一切实数x、y,关系式:f(x-y)=f(x)-(2x-y+1)y,且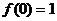 ,求函数f(x)的表达式.
,求函数f(x)的表达式.
4、定义在(0,+∞)上的增函数f(x)满足: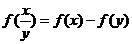
⑴求证:f(1)=0
⑵求证:f(xn)=nf(x)
⑶如果f(3)=1,解不等式: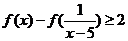
三、课堂练习:
1、如果函数f(x)的定义域为R+且满足:f(xy)=f(x)
+f(y),f(8)=3,那么f(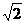 )=
.
)=
.
2、已知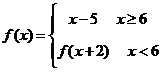 ,那么f(3)=………………………………………………( )
,那么f(3)=………………………………………………( )
(A)5 (B)4 (C)3 (D)2
四、课堂小结:
1、 解析式只是表示一种对应关系,与具体的字母无关。如y=2x+1与u=2t+1是同一函数;
2、 求函数的解析式的方法一般有:待定系数法、换元法,在已知表达式比较简单时可以用拼凑法求解.
3、 用赋值法处理抽象函数(即表达式不知道的函数)是一种常见方法.
五、能力测试: 姓名 得分
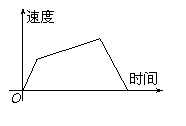 1、某运动的速度曲线如右图,从以下的运动中选出一种,其速度变
1、某运动的速度曲线如右图,从以下的运动中选出一种,其速度变
化最符合图中的曲线…………………………………………( )
(A) 钓鱼 (B)跳高 (C)100米跑 (D)掷标枪
2、点A(x,y)在曲线y=log2(x+1)上运动时,点B(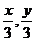 )在曲线y=
)在曲线y=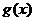
上运动,则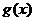 = .
= .
3、函数y=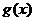 的图象关于直线x=-1对称,且x∈(0,+∞)时,
的图象关于直线x=-1对称,且x∈(0,+∞)时,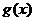 =
=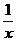 ,那么x∈(-∞,-2)时
,那么x∈(-∞,-2)时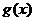 =
.
=
.
4、设函数f(x)的定义域为R且满足x1≠x2则f(x1)≠f(x2),又对任何实数x、y总有:f(x+y)=f(x) f(y),证明:⑴f(0)=1 ⑵f(x)>0恒成立.
5、对一切非0实数x、y满足:f(xy)=f(x) +f(y)
⑴求证:f(1)=f(-1)=0
⑵判断f(x)的奇偶性
⑶如果f(x)在(0,+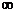 )上递增,解不等式
)上递增,解不等式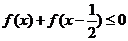
6、对任意实数x,若y=f(x)是y=2-x2和y=x这两个函数中的较小者,求函数y=f(x)的解析式.
2.9 函数的图象
〖考纲要求〗能利用函数的性质与图象的对称性描绘简单函数的图象
〖复习要求〗掌握用描点法和图象变换法描绘函数的草图,能利用函数图象解决有关问题.
〖复习建议〗记住基本初等函数的图象特征,能利用函数图象研究函数的定义域、值域、单调性、奇偶性、周期性、对称性以及一些特殊函数值等,掌握函数图象的三种基本变换:平移变换、对称变换、伸缩变换,要能运用数形结合的思想方法解决有关问题(讨论函数的性质、确定方程解的个数、解不等式……)
〖双基回顾〗
1、将函数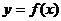 的图象平移a个单位,求所得的函数解析式:
的图象平移a个单位,求所得的函数解析式:
⑴向右平移 ⑵向左平移
⑶向上平移 ⑷向下平移
2、函数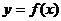 的图象关于下列元素对称的图象对应函数解析式:
的图象关于下列元素对称的图象对应函数解析式:
⑴x轴 ⑵y轴 ⑶原点
⑷直线y=x ⑸直线y+x=0 .
3、将函数 的图象向左平移一个单位得C1,再作C1关于y轴的对称曲线C2,将C2向下平移两个单位得C3,作C3关于直线y=x的对称曲线C4,那么C4的方程为
.
的图象向左平移一个单位得C1,再作C1关于y轴的对称曲线C2,将C2向下平移两个单位得C3,作C3关于直线y=x的对称曲线C4,那么C4的方程为
.
 4、下列函数,分别对应四个图象,其中解析式与图象对应错误的是…………………………( )
4、下列函数,分别对应四个图象,其中解析式与图象对应错误的是…………………………( )
*5、函数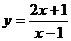 图象的对称中心为
.
图象的对称中心为
.
一、典型例题分析:
1、函数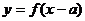 与函数
与函数 的图象关于……………………………………( )对称
的图象关于……………………………………( )对称
(A)x轴 (B)y轴 (C)直线x=a (D)直线y=a.
2、方程2x+x3=0的实数解的个数为………………………………………………………………( )
(A)0 (B)1 (C)2 (D)3
3、作下列函数的图象,并且根据图象说出其单调区间
⑴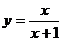 ⑵y=x(|x|-2) ⑶y=|x-1|+|2x+3|
⑵y=x(|x|-2) ⑶y=|x-1|+|2x+3|
4、讨论方程 的实数根的个数.
的实数根的个数.
*5、函数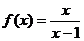
⑴求使 为整数的所有整数x的值.
为整数的所有整数x的值.
⑵如果圆心在原点的圆与函数的图象有三个交点,求此圆的半径.
⑶求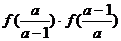 的最大值.
的最大值.
二、课堂练习:
1、判断下列命题是否正确:
(1)奇函数的图象一定过原点; (2)函数y=f(x)的图象与函数x=f(y)的图象关于直线y=x对称;
(3)若函数f(x)=f(-x),则f(x)的图象关于y轴对称; (4)y=f(x)图象与y=-f(x)图象关于x轴对称
2、函数 =log2|ax-1|的图象关于直线x=2对称,那么实数a=
.
=log2|ax-1|的图象关于直线x=2对称,那么实数a=
.
3、函数y= 的图象过点(0,1),则函数
的图象过点(0,1),则函数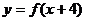 的反函数的图象一定经过…………( )
的反函数的图象一定经过…………( )
(A)(4,-1) (B)(1,-4) (C)(-4,1) (D)(1,4)
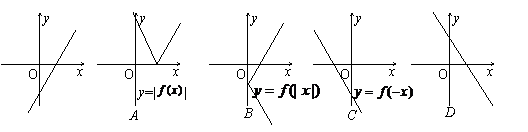 4、 函数y=
4、 函数y= 的图象如下,那么下列对应错误的是…………………………………………( )
的图象如下,那么下列对应错误的是…………………………………………( )
|
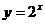 的图象…………………………………………………………………………………… ( )
的图象…………………………………………………………………………………… ( )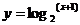 的图象.
的图象. (B)
(B)
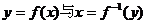 (D)
(D) 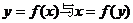
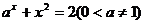 的解的个数………………………………………………………( )
的解的个数………………………………………………………( )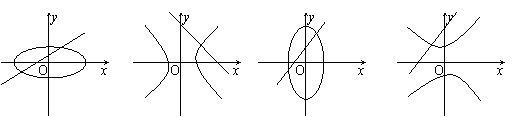 6、方程
6、方程 与mx+ny=1在同一坐标系内的图象为……………………………………( )
与mx+ny=1在同一坐标系内的图象为……………………………………( ) 对称 (D) 关于直线x=2a对称
对称 (D) 关于直线x=2a对称 ,且
,且 ,
, ,现在该商场准备用3万元资金经营这两种商品.试问,应该对甲,乙两种商品分别投入多少资金,才能使经营这两种商品的总利润最大,并求这总利润是多少万元?.
,现在该商场准备用3万元资金经营这两种商品.试问,应该对甲,乙两种商品分别投入多少资金,才能使经营这两种商品的总利润最大,并求这总利润是多少万元?.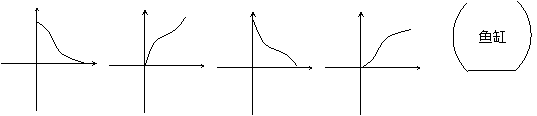 1、一个高为H,水量为V的鱼缸的轴截面如图,其底部有一个洞,满缸水从洞中流出,如果水深为h时水的体积为v,则函数
1、一个高为H,水量为V的鱼缸的轴截面如图,其底部有一个洞,满缸水从洞中流出,如果水深为h时水的体积为v,则函数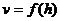 的大致图象是……………………………………………( )
的大致图象是……………………………………………( )
 给出,其中m>0,[m]表示不大于m的最小正整数,那么从甲地到已地通话5.5分钟的话费为……………………( )
给出,其中m>0,[m]表示不大于m的最小正整数,那么从甲地到已地通话5.5分钟的话费为……………………( ) 4、有一面足够长的墙,现用一36米长的篱笆围成如图所示的四个面积相等的猪圈,那么猪圈的最大总面积为
.
4、有一面足够长的墙,现用一36米长的篱笆围成如图所示的四个面积相等的猪圈,那么猪圈的最大总面积为
.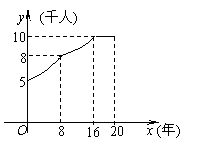 3、某集镇近20年常住人口y(千人)与时间x(年)
3、某集镇近20年常住人口y(千人)与时间x(年)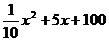 (元),而出售x吨这种商品时,每吨的售价为P元,这里P依关系式
(元),而出售x吨这种商品时,每吨的售价为P元,这里P依关系式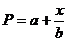 (a,b为常数)而定.如果生产出来的这种产品都能卖完,那么当产量是150吨时,所获利润最大,并且这时每吨的价格为40元,求a,b的值.
(a,b为常数)而定.如果生产出来的这种产品都能卖完,那么当产量是150吨时,所获利润最大,并且这时每吨的价格为40元,求a,b的值. (
( )方向300km的海面P处,并且以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并且以10km/h的速度不断增大,问几个小时后,该城市开始受到台风的侵袭?
)方向300km的海面P处,并且以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并且以10km/h的速度不断增大,问几个小时后,该城市开始受到台风的侵袭?
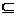 A,那么a=………………………………………( )
A,那么a=………………………………………( )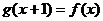 ,那么
,那么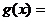 ………………………………………………( )
………………………………………………( )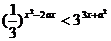 恒成立,则实数a的取值范围是………………( )
恒成立,则实数a的取值范围是………………( )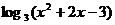 的单调递减区间是…………………………………………………( )
的单调递减区间是…………………………………………………( )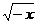 +1
(B) ―
+1
(B) ―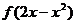 的递增区间是………………………( )
的递增区间是………………………( )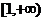 (C)
(C) 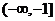 (D)
(D) 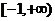
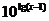 图象相同的函数是………………………………………………………( )
图象相同的函数是………………………………………………………( )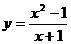 (D)
(D)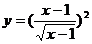
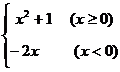 并且
并且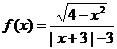 的奇偶性是
.
的奇偶性是
.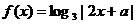 的图象关于直线x=2对称,那么a=
.
的图象关于直线x=2对称,那么a=
.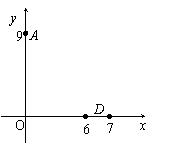 17、在如图所示的直角坐标系中,一个运动物体经过点A(0,9),其轨迹方
17、在如图所示的直角坐标系中,一个运动物体经过点A(0,9),其轨迹方  ,如果B
,如果B 20、某公司今年初推出一种新产品,每件产品成本价为452元,经过市场2~6月份调查,其销售价与销售量的关系为:
20、某公司今年初推出一种新产品,每件产品成本价为452元,经过市场2~6月份调查,其销售价与销售量的关系为: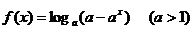
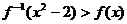
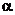 ,
, 为何实数,恒有:
为何实数,恒有: