摘要：掌握好图象问题的关键是:熟悉基本函数的图象.掌握一些常见的结论.
网址：http://m.1010jiajiao.com/timu_id_177323[举报]
已知函数f(x)=2sin2x+sin2x,x∈R.
(1)求函数f(x)的最大值、最小值及单调增区间;
(2)函数f(x)的图象是由函数y=sinx,x∈R的图象经过怎样的变换而得到的?
分析:解此类问题的关键是把函数f(x)转化成一个角的一个三角函数的形式.
查看习题详情和答案>>
（1）已知函数f（x）=-x2+4（x∈（-1，2）），P、Q是f（x）图象上的任意两点．
①试求直线PQ的斜率kPQ的取值范围；
②求f（x）图象上任一点切线的斜率k的范围；
（2）由（1）你能得出什么结论？（只须写出结论，不必证明），试运用这个结论解答下面的问题：已知集合MD是满足下列性质函数f（x）的全体：若函数f（x）的定义域为D，对任意的x1，x2∈D，（x1≠x2）有|f（x1）-f（x2）|＜|x1-x2|．
①当D=（0，1）时，f（x）=lnx是否属于MD，若属于MD，给予证明，否则说明理由；
②当D=(0，
)，函数f（x）=x3+ax+b时，若f（x）∈MD，求实数a的取值范围．
查看习题详情和答案>>
①试求直线PQ的斜率kPQ的取值范围；
②求f（x）图象上任一点切线的斜率k的范围；
（2）由（1）你能得出什么结论？（只须写出结论，不必证明），试运用这个结论解答下面的问题：已知集合MD是满足下列性质函数f（x）的全体：若函数f（x）的定义域为D，对任意的x1，x2∈D，（x1≠x2）有|f（x1）-f（x2）|＜|x1-x2|．
①当D=（0，1）时，f（x）=lnx是否属于MD，若属于MD，给予证明，否则说明理由；
②当D=(0，
| ||
| 3 |
某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图象（部分）刻画了该公司年初以来累积利润s（万元）与销售时间t（月）之间的关系（即前t个月的利润总和s与t之间的关系）．根据图象提供的信息解答下列问题：（1）由已知图象上的三点坐标，求累积利润s（万元）与时间t（月）之间的函数关系式；
（2）求截止到第几月末公司累积利润可达到30万元；
（3）求第八个月该公司所获利润是多少万元？
某校高一年级数学兴趣小组的同学经过研究，证明了以下两个结论是完全正确的：①若函数y=f（x）的图象关于点P（a，b）成中心对称图形，则函数y=f（x+a）-b是奇函数；②若函数y=f（x+a）-b是奇函数，则函数y=f（x）的图象关于点P（a，b）成中心对称图形．请你利用他们的研究成果完成下列问题：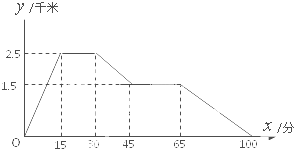
如图的图象反映的过程是：