21、(2011•潍坊)2010年秋冬北方严重干早,凤凰社区人畜饮用水紧张.毎天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂毎天最多可调出80吨,乙厂毎天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:
|
|
到凤凰社区供水点的路程(千米) |
运费(元/吨•千米) |
|
甲厂 |
20 |
12 |
|
乙厂 |
14 |
15 |
(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元.试写出W关于与x的函数关系式,怎样安排调运方案才能使毎天的总运费最省?
考点:一次函数的应用;二元一次方程组的应用;一元一次不等式的应用。
专题:优选方案问题。
分析:(1)设设从甲厂调运了x吨饮用水,从甲厂调运了y吨饮用水,然后根据题意毎天需从社区外调运饮用水120吨与某天调运水的总运费为26700元列方程组即可求得答案;
(2)首先根据题意求得一次函数W=20×12x+14×15(120﹣x),又由甲厂毎天最多可调出80吨,乙厂毎天最多可调出90吨,确定x的取值范围,则由一次函数的增减性即可求得答案.
解答:解:(1)设从甲厂调运了x吨饮用水,从甲厂调运了y吨饮用水,
由题意得: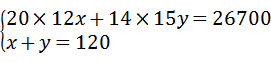 ,
,
解得: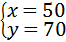 ,
,
∵50≤80,70≤90,
∴符合条件,
∴从甲、乙两水厂各调运了50吨、0吨吨饮用水;
(2)从甲厂调运饮用水x吨,则需从乙调运水120﹣x吨,
∵x≤80,且120﹣x≤90,
∴30≤x≤80,
总运费W=20×12x+14×15(120﹣x)=30x+25200,
∵W随X的增大而增大,
∴当x=30时,W最小=26100元,
∴每天从甲厂调运30吨,从乙厂调运90吨,每天的总运费最省.
点评:此题考查了二元一次方程组与一次函数的实际应用.此题难度适中,解题的关键是理解题意,抓住等量关系.
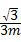 (x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)
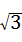 m).
m).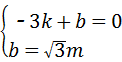 解得,k=
解得,k=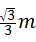 ,b=
,b=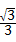 mx+
mx+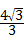 m.
m.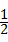 AE.•OD=
AE.•OD=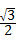 m(3﹣m)
m(3﹣m)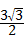 m.
m.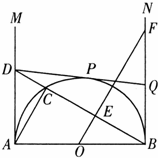

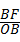 =
=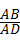 ,
,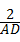 ,
,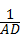 ,
,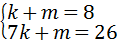 解之得:
解之得: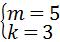
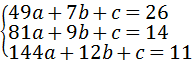 解之得:
解之得: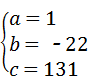
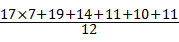 ≈15.3元/千克,
≈15.3元/千克,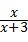 ,
,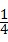 ;
;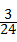 =
=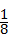 .
.


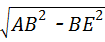 =
=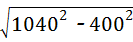 =960米,
=960米,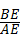 =
=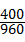 =
=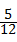 ,故斜坡AB的坡度为1:2.4.
,故斜坡AB的坡度为1:2.4.
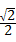 a.
a.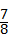 cm .
cm .

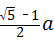 .
.
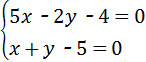 的解是
的解是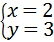 .
.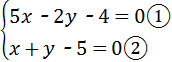 ,②×2+①得,7x﹣14=0,解得x=2;
,②×2+①得,7x﹣14=0,解得x=2;