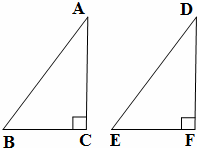
19、(2011•达州)在△ABC和△DEF中,∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤,其正面分别写有五个不同的等式,小民将这五张纸牌背面朝上洗匀后先随机摸出一张(不放回),再随机摸出一张.请结合以上条件,解答下列问题.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用①、②、③、④、⑤表示);
(2)用两次摸牌的结果和∠C=∠F=90°作为条件,求能满足△ABC和△DEF全等的概率.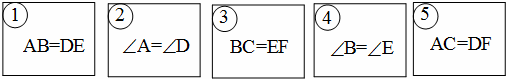
考点:列表法与树状图法;全等三角形的判定。
专题:计算题。
分析:(1)两两组合,列出表格将所有可能一一列举出来即可;
(2)利用全等三角形的判定将所有能组成全等三角形的条件列举出来,求得概率即可.
解答:解:(1)列表如下;
|
|
① |
② |
③ |
④ |
⑤ |
|
① |
|
①② |
①③ |
①④ |
①⑤ |
|
② |
②① |
|
②③ |
②④ |
②⑤ |
|
③ |
③① |
③② |
|
③④ |
③⑤ |
|
④ |
④① |
④② |
④③ |
|
④⑤ |
|
⑤ |
⑤① |
⑤② |
⑤③ |
⑤④ |
|
∴两次摸牌所有可能出现的结果共有20种
(用树状图解参照给分)
(2)两次摸牌所有可能出现的结果共有20种,其中满足△ABC≌△DEF的有18种可能,
∴P(能满足△ABC≌△DEF)=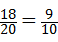
点评:本题考查了列表法和树状图法求概率及全等三角形的判定.树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.
12、(2011•达州)我市某中学七年级甲、乙、丙三个班中,每班的学生人数都为60名,某次数学考试的成绩统计如下:(每组分数含最小值,不含最大值)
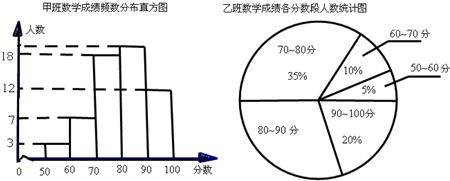
丙班数学成绩频数统计表
|
分数 |
50-60 |
60-70 |
70-80 |
80-90 |
90-100 |
|
人数 |
2 |
9 |
18 |
17 |
14 |
根据以上图、表提供的信息,则80-90分这一组人数最多的班是 甲班 .
考点:频数(率)分布直方图;扇形统计图。
分析:从直方图可求出甲班80-90的人数,从扇形图求出乙班这个范围内的人数,从频数统计表可求出丙班的,从而可求出总人数.
解答:解:甲班:60﹣3﹣7﹣12﹣18=20(人)
乙班:60×(1﹣35%﹣10%﹣5%﹣20%)=18(人).
丙班:17(人).
所以最多的是甲班.
点评:本题考查频数直方图,扇形图以及频数表的认知能力,关键知道直方图能够直接看出每组的人数,扇形图看出每部分占总体的百分比,频数表中频数就是每组的人数.
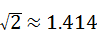 ,
,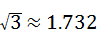 )
)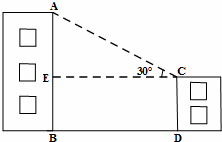
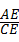
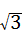 ≈34.64(米),
≈34.64(米),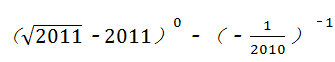
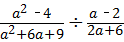 ,其中a=﹣5.
,其中a=﹣5.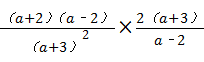 ,(1分)
,(1分)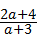 ,(2分)
,(2分)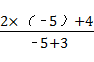 ,(3分)
,(3分)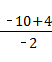 ,
,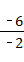 ,
,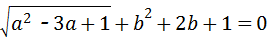 ,则
,则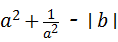 = 6 .
= 6 .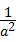 、b的值,再代入计算即可.
、b的值,再代入计算即可.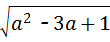 +(b+1)2=0,
+(b+1)2=0,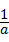 =3,a2+
=3,a2+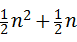 )(或
)(或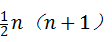 ) 个(用含n的代数式表示).
) 个(用含n的代数式表示).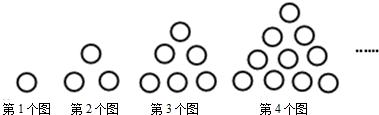
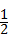 ×1×(1+1)
×1×(1+1)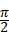 (结果不取近似值).
(结果不取近似值).
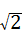 ,
,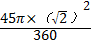 ×2,
×2,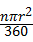 .
.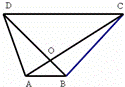
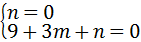 ,
,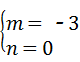 .
.