0 49601 49609 49615 49619 49625 49627 49631 49637 49639 49645 49651 49655 49657 49661 49667 49669 49675 49679 49681 49685 49687 49691 49693 49695 49696 49697 49699 49700 49701 49703 49705 49709 49711 49715 49717 49721 49727 49729 49735 49739 49741 49745 49751 49757 49759 49765 49769 49771 49777 49781 49787 49795 447348
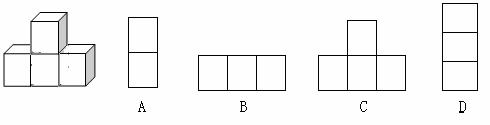
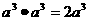 B
B 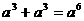 C
C 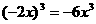 D
D 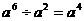
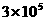 B
B 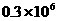 C
C 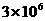 D
D 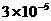
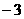 的相反数是( )
的相反数是( )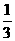 B
B 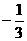 C 3 D
C 3 D 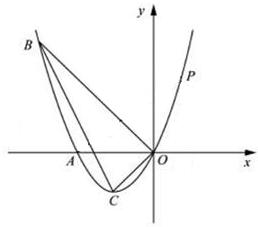
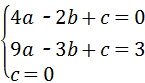 ,
,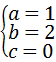 .
.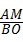 =
=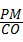 ,
,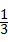 ,x2=﹣2(舍去).
,x2=﹣2(舍去).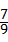 ,即P(
,即P(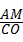 =
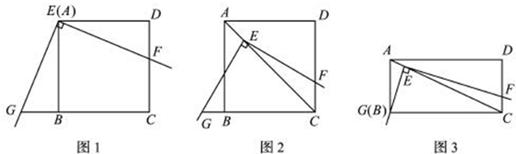
=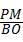 ,
,
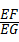 的值.
的值.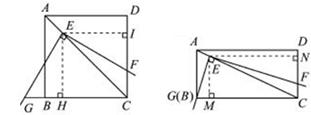
 ,
,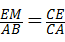 ,
,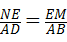 ,即
,即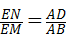 =
=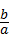 ,
,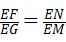 ,
,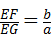 .
.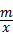 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
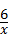 ,
,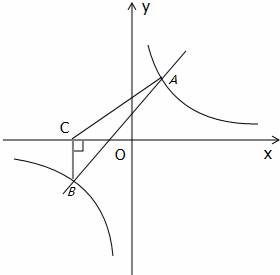 ∴n=
∴n=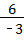 =﹣2,
=﹣2,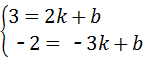 ,
,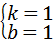 ,
,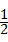 ×2×5=5.
×2×5=5.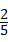 ,AC=
,AC=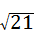 .
.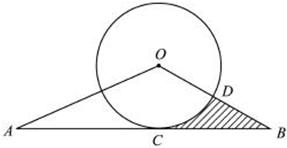
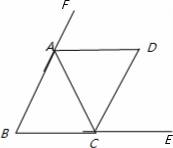
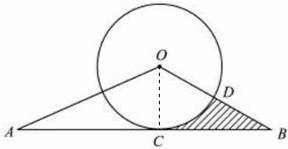 (1)连接OA,
(1)连接OA,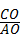 ,
,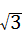 ,
,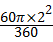 =2
=2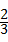 π.
π.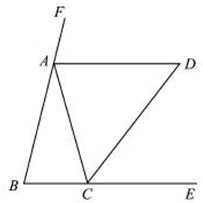
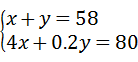 ,
,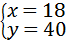 .
.