0 49651 49659 49665 49669 49675 49677 49681 49687 49689 49695 49701 49705 49707 49711 49717 49719 49725 49729 49731 49735 49737 49741 49743 49745 49746 49747 49749 49750 49751 49753 49755 49759 49761 49765 49767 49771 49777 49779 49785 49789 49791 49795 49801 49807 49809 49815 49819 49821 49827 49831 49837 49845 447348
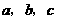 为
为 的三个内角
的三个内角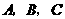 的对边,向量
的对边,向量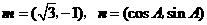 .若
.若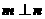 ,且
,且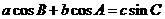 ,则角
,则角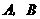 的大小分别为( )
的大小分别为( )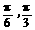 B.
B.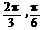 C.
C.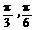 D.
D.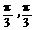
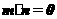 即
即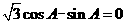 所以角
所以角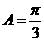 ,
,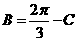 可得
可得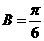
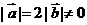 ,且关于
,且关于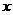 的方程
的方程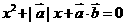 有实根,则
有实根,则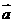 与
与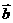 的夹角的取值范围是 ( )
的夹角的取值范围是 ( )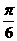 ] B.
] B.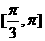 C.
C.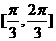 D.
D.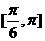
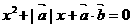 有实根,得:
有实根,得: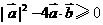
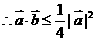 .设向量
.设向量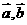 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=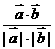 ,又
,又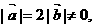
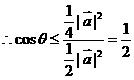 ,∴θ∈
,∴θ∈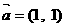 ,
,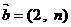 ,若
,若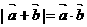 ,则
,则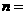 ( )
( ) 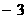 B.
B.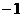 C.
C.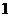 D.
D.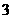
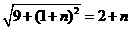 解得
解得 ·
·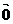 =
=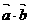 ,不能写成
,不能写成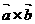 ,也不能写成
,也不能写成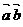 (所以有时把数量积称为“点乘”,记号
(所以有时把数量积称为“点乘”,记号 =0却不能得出
=0却不能得出 ⑵ 若a、b、c∈R,且a≠0,则由ab=ac可得b=c,但由
⑵ 若a、b、c∈R,且a≠0,则由ab=ac可得b=c,但由 及
及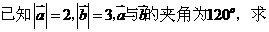
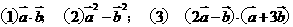 ;
;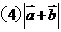
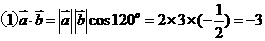 解析:
解析: 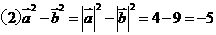
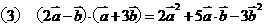
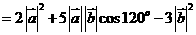
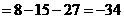
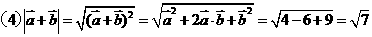
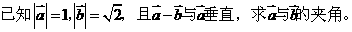
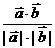 。
。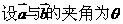
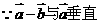
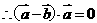
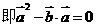
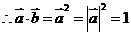
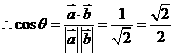
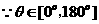
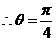
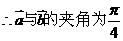
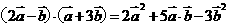 ,当知道
,当知道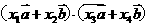 的数量积,反之知道
的数量积,反之知道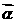 、
、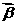 满足
满足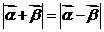 ,证明:
,证明: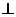
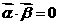 。
。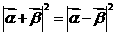
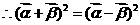
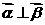
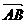 =(2, 3),
=(2, 3),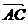 =(1, k),且△ABC的一个内角为直角,
=(1, k),且△ABC的一个内角为直角,
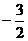
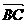 = 0,
= 0,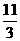
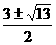
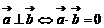 是一个常用的结论。
是一个常用的结论。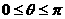 ) cosq =
) cosq = 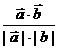
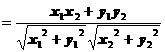
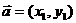 ,
,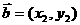 ,则
,则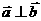

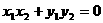
 的有向线段的起点和终点的坐标分别为
的有向线段的起点和终点的坐标分别为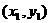 、
、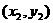 ,
,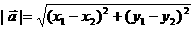
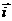 是
是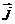 是
是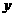 轴上的单位向量,那么
轴上的单位向量,那么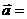
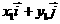 ,
, 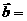
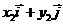 所以
所以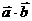
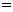
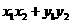
 =
= 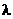
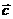 =
=