0 49509 49517 49523 49527 49533 49535 49539 49545 49547 49553 49559 49563 49565 49569 49575 49577 49583 49587 49589 49593 49595 49599 49601 49603 49604 49605 49607 49608 49609 49611 49613 49617 49619 49623 49625 49629 49635 49637 49643 49647 49649 49653 49659 49665 49667 49673 49677 49679 49685 49689 49695 49703 447348


 中,AB=2OA=20,BC=16,∴
中,AB=2OA=20,BC=16,∴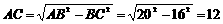
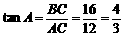 ∴
∴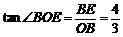
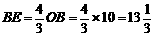 .
.
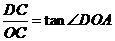 =
=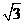 ,
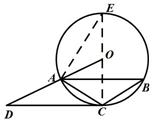
,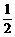 ,求sinE的值.
,求sinE的值.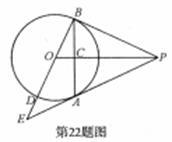
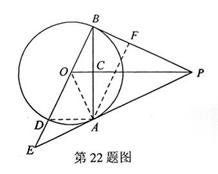
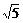 t 过A作AF⊥PB于F,则AF·PB=AB·PC
t 过A作AF⊥PB于F,则AF·PB=AB·PC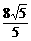 t 进而由勾股定理得PF=
t 进而由勾股定理得PF=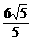 t
t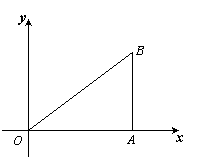

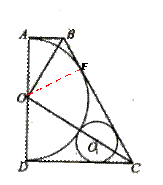
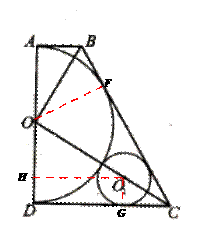
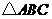 ,以
,以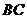 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点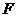 ,点
,点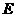 为
为
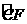 的中点,连接
的中点,连接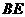 交
交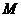 ,
,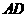 为
为 的角平分线,且
的角平分线,且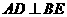 ,垂足为点
,垂足为点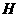 。
。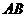 是半圆
是半圆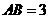 ,
,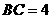 ,求
,求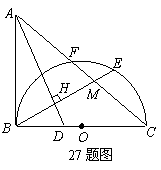

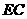 ,
,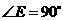
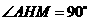
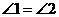 ∴
∴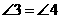
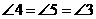
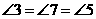
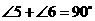 即
即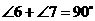
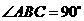 ,∴
,∴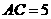 。
。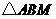 中,
中,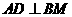 于
于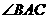 ,
,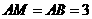 ,∴
,∴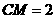 。
。 ∽
∽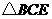 ,得
,得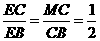 。
。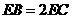 ,
,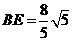 。
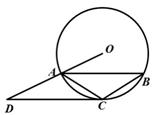
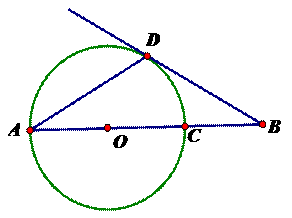
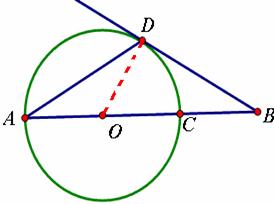
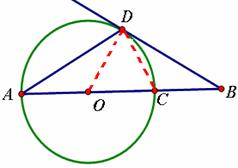
。 O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.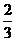 ,求BE的长
,求BE的长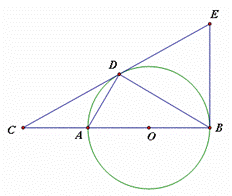
 .若cos
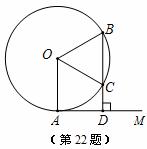
.若cos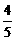 .OQ= 15.求AB的长
.OQ= 15.求AB的长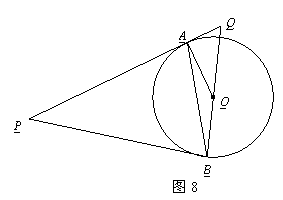

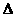 QOA
QOA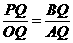 即AQ·PQ= OQ·BQ
即AQ·PQ= OQ·BQ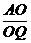 =
=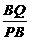 =
=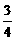 ∴PB=36 PO=12
∴PB=36 PO=12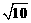
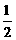 AB·PO= OB·BP ∴AB=
AB·PO= OB·BP ∴AB=