摘要:如图.AB是半径O的直径.AB=2.射线AM.BN为半圆O的切线.在AM上取一点D.连接BD交半圆于点C.连接AC.过O点作BC的垂线OE.垂足为点E.与BN相交于点F.过D点作半圆O的切线DP.切点为P.与BN相交于点Q. (1)求证:△ABC∽△OFB, (2)当△ABD与△BFO的面枳相等时.求BQ的长, (3)求证:当D在AM上移动时.点Q始终是线段BF的中点. 考点:切线的性质,全等三角形的判定与性质,勾股定理,圆周角定理,相似三角形的判定与性质. 专题:证明题,几何综合题. 分析:(1)根据OE∥AC.得出∠BAC=∠FOB.进而得出∠BCA=∠FBO=90°.从而证明结论, (2)根据△ACB∽△OBF得出△ABD∽△BFO.从而得出DQ∥AB.即可得出BQ=AD, (3)首先得出AD=DP.QB=BQ.进而得出DQ2=QK2+DK2.得出BF=2BQ.即可得出Q为BF的中点. 解答:证明:(1)∵AB为直径. ∴∠ACB=90°.即:AC⊥BC. 又OE⊥BC. ∴OE∥AC. ∴∠BAC=∠FOB. ∵BN是半圆的切线. ∴∠BCA=∠FBO=90°. ∴△ACB∽△OBF. 解:(2)由△ACB∽△OBF得.∠OFB=∠DBA.∠DAB=∠OBF=90°. ∴△ABD∽△BFO. 当△ABD与△BFO的面积相等时.△ABD≌△BFO. ∴AD=1. 又DPQ是半圆O的切线. ∴OP=1.且OP⊥DP. ∴DQ∥AB. ∴BQ=AD=1. 知.△ABD∽△BFO. ∴=. ∴BF=. ∵DPQ是半圆O的切线. ∴AD=DP.QB=BQ. 过Q点作AM的垂线QK.垂足为K.在直角三角形DQK中. DQ2=QK2+DK2. ∴2=2+22. ∴BQ=. ∴BF=2BQ. ∴Q为BF的中点. 点评:此题主要考查了切线的性质以及全等三角形的判定和相似三角形的判定等知识.熟练利用相似三角形的判定是解决问题的关键.
网址:http://m.1010jiajiao.com/timu3_id_496959[举报]
(2011•潍坊)如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.
(2011•潍坊)如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
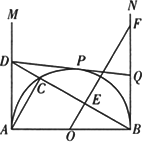
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.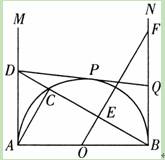
(1)求证:△ABC∽△OFB;
(2)当△ABD与△BFO的面枳相等时,求BQ的长;
(3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点.

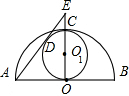 如图,AB是半圆O的直径,半径OC⊥AB,⊙O1的直径是OC,AD切⊙O1于D,交OC的延长线于E,设⊙O1的半径为r=3,则DE=
如图,AB是半圆O的直径,半径OC⊥AB,⊙O1的直径是OC,AD切⊙O1于D,交OC的延长线于E,设⊙O1的半径为r=3,则DE= 段PC于点E,且PD=PE.
段PC于点E,且PD=PE.