8.已知等差数列{an}中,a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19,n∈N*)成立,那么等比数列{bn}中,若b9=1,则有等式________成立.
解析:这是一个由等差数列与等比数列类比的题目,由于二者的参照物不同,因此我们要先进行分析,从二者的本质即数列的结构找到突破口,如下表所示:
|
特征 |
等差数列 |
等比数列 |
|
运算符号 |
和(差) |
积(商) |
|
通项 |
an |
bn |
|
公差(比) |
d |
q |
|
前n项和 |
Sn |
Tn |
|
特殊项 |
0 |
1 |
|
等式结构 |
左边n项, 右边19-n项 |
左边n项, 右边17-n项 |
|
符号转换 |
加法 |
乘法 |
|
减法 |
除法 |
|
|
关键词 |
a10=0 |
b9=1 |
由题设,若ak=0,那么有a1+a2+…+an=a1+a2+…+a2k-1-n(n<2k-1,n∈N*)成立.由等差数列与等比数列的加乘转换性质,我们可以类比得出这样的结论:b1b2·…·bn=b1b2·…·b2k-1-n(n<2k-1,n∈N*)成立.结合本题k=9,得2k-1-n=17-n,故本题应填:b1b2·…·bn=b1b2·…·b17-n(n<17,n∈N*).
答案:b1b2·…·bn=b1b2·…·b17-n(n<17,n∈N*)
评析:本题为往年一高考题,类比结论有较高的难度,本题易出现的错误是多方面的,可能仍然写成和的形式,也可能不会应用b9=1这一条件进行类比.
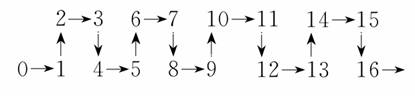
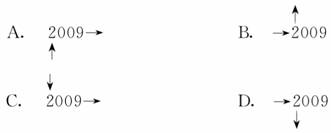
 ,故选B.
,故选B.