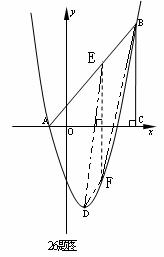
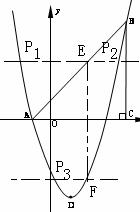
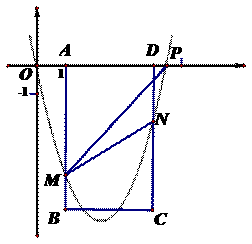
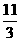35. (2011重庆市潼南,26,12分)如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,
OC=4,抛物线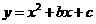 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线
交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上
是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的
坐标;若不存在,说明理由.
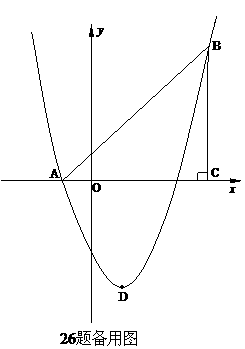
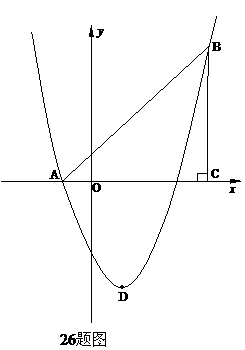
[答案]解:(1)由已知得:A(-1,0) B(4,5)------------1分
 ∵二次函数
∵二次函数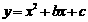 的图像经过点A(-1,0)B(4,5)
的图像经过点A(-1,0)B(4,5)
∴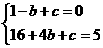 ------------2分
------------2分
解得:b=-2 c=-3 ------------3分
(2如26题图:∵直线AB经过点A(-1,0) B(4,5)
∴直线AB的解析式为:y=x+1
∵二次函数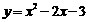
∴设点E(t, t+1),则F(t,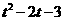 ) ------------4分
) ------------4分
∴EF= 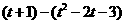 ------------5分
------------5分
=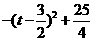
 ∴当
∴当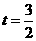 时,EF的最大值=
时,EF的最大值=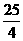
∴点E的坐标为(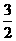 ,
,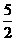 ) ------------------------6分
) ------------------------6分
(3)①如26题图:顺次连接点E、B、F、D得四边形EBFD.
可求出点F的坐标(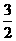 ,
,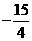 ),点D的坐标为(1,-4)
),点D的坐标为(1,-4)
S = S
= S + S
+ S
=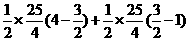
|
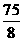 -----------------------------------9分
-----------------------------------9分
②如26题备用图:ⅰ)过点E作a⊥EF交抛物线于点P,设点P(m,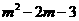 )
)
则有: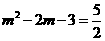 解得:
解得: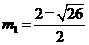 ,
,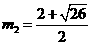
∴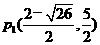 ,
, 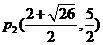
ⅱ)过点F作b⊥EF交抛物线于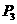 ,设
,设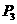 (n,
(n,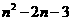 )
)
则有: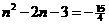 解得:
解得: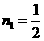 ,
,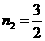 (与点F重合,舍去)∴
(与点F重合,舍去)∴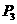
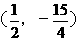
综上所述:所有点P的坐标: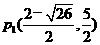 ,
,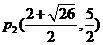
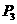 (
( . 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
. 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
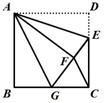
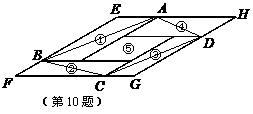
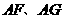 分别架在墙体的点
分别架在墙体的点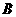 、点
、点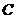 处,且
处,且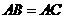 ,侧面四边形
,侧面四边形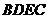 为矩形,若测得
为矩形,若测得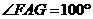 ,则
,则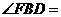 ( )
( )

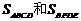 .现给出下列命题:( )
.现给出下列命题:( )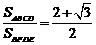 ,则
,则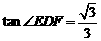 .②若
.②若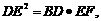 则
则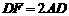 .
.
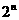 (B)
(B)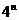 (C)
(C)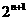 (D)
(D)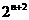
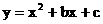 经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).
经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).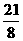 ;
;
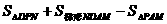
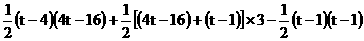
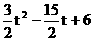
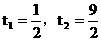
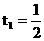 舍去,∴t=
舍去,∴t=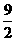
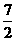 <t<
<t<