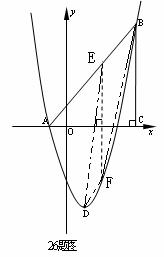
26. 解:(1)由已知得:A(-1,0) B(4,5)------------1分
 ∵二次函数
∵二次函数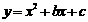 的图像经过点A(-1,0)B(4,5)
的图像经过点A(-1,0)B(4,5)
∴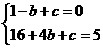 ------------2分
------------2分
解得:b=-2 c=-3 ------------3分
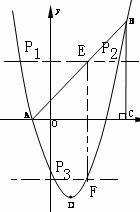
(2如26题图:∵直线AB经过点A(-1,0) B(4,5)
∴直线AB的解析式为:y=x+1
∵二次函数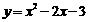
∴设点E(t, t+1),则F(t,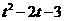 ) ------------4分
) ------------4分
∴EF= 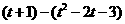 ------------5分
------------5分
=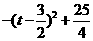
 ∴当
∴当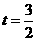 时,EF的最大值=
时,EF的最大值=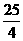
∴点E的坐标为(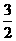 ,
,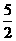 ) ------------------------6分
) ------------------------6分
(3)①如26题图:顺次连接点E、B、F、D得四边形EBFD.
可求出点F的坐标(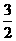 ,
,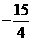 ),点D的坐标为(1,-4)
),点D的坐标为(1,-4)
S = S
= S + S
+ S
=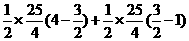
|
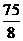 -----------------------------------9分
-----------------------------------9分
②如26题备用图:ⅰ)过点E作a⊥EF交抛物线于点P,设点P(m,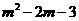 )
)
则有: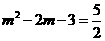 解得:
解得: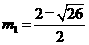 ,
,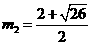
∴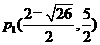 ,
, 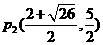
ⅱ)过点F作b⊥EF交抛物线于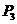 ,设
,设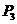 (n,
(n,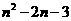 )
)
则有: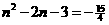 解得:
解得: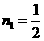 ,
,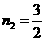 (与点F重合,舍去)∴
(与点F重合,舍去)∴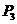
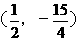
综上所述:所有点P的坐标: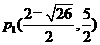 ,
,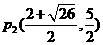
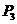 (
(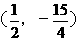 . 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
. 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
(江苏省宿迁市2011年)26.(本题满分10分)如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=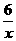 (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积;
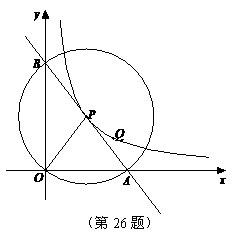 (3)Q是反比例函数y=
(3)Q是反比例函数y=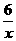 (x>0)图象上异于点P的另一点,请以Q为圆心,QO
(x>0)图象上异于点P的另一点,请以Q为圆心,QO
半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
解:(1)点P在线段AB上,理由如下:
∵点O在⊙P上,且∠AOB=90°
∴AB是⊙P的直径
∴点P在线段AB上.
(2)过点P作PP1⊥x轴,PP2⊥y轴,由题意可知PP1、PP2
是△AOB的中位线,故S△AOB=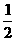 OA×OB=
OA×OB=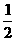 ×2 PP1×PP2
×2 PP1×PP2
∵P是反比例函数y=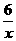 (x>0)图象上的任意一点
(x>0)图象上的任意一点
∴S△AOB=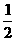 OA×OB=
OA×OB=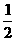 ×2 PP1×2PP2=2 PP1×PP2=12.
×2 PP1×2PP2=2 PP1×PP2=12.
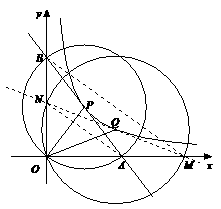 (3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
(3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
∴OA·OB=OM·ON
∴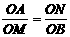
∵∠AON=∠MOB
∴△AON∽△MOB
∴∠OAN=∠OMB
∴AN∥MB.
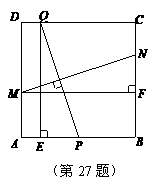
(江苏省宿迁市2011年)27.(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 解:(1)∵四边形ABCD是正方形
解:(1)∵四边形ABCD是正方形
∴∠A=∠B=∠D=90°,AD=AB
∵QE⊥AB,MF⊥BC
∴∠AEQ=∠MFB=90°
∴四边形ABFM、AEQD都是矩形
∴MF=AB,QE=AD,MF⊥QE
又∵PQ⊥MN
∴∠EQP=∠FMN
又∵∠QEP=∠MFN=90°
∴△PEQ≌△NFM.
(2)∵点P是边AB的中点,AB=2,DQ=AE=t
∴PA=1,PE=1-t,QE=2
由勾股定理,得PQ=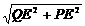 =
=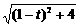
∵△PEQ≌△NFM
∴MN=PQ=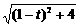
又∵PQ⊥MN
∴S=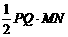 =
=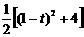 =
=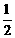 t2-t+
t2-t+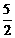
∵0≤t≤2
∴当t=1时,S最小值=2.
综上:S=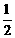 t2-t+
t2-t+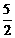 ,S的最小值为2.
,S的最小值为2.
(江苏省宿迁市2011年)28.(本题满分12分)如图,在Rt△ABC中,∠B=90°,AB=1,BC=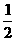 ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
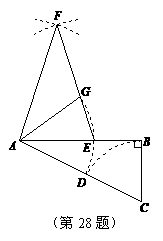 (2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
解:(1)在Rt△ABC中,由AB=1,BC=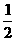 得 AC=
得 AC=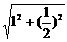 =
=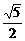
∵BC=CD,AE=AD
∴AE=AC-AD=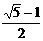 .
.
(2)∠EAG=36°,理由如下:
∵FA=FE=AB=1,AE=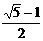
∴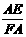 =
=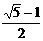
∴△FAE是黄金三角形
∴∠F=36°,∠AEF=72°
∵AE=AG,FA=FE
∴∠FAE=∠FEA=∠AGE
∴△AEG∽△FEA
∴∠EAG=∠F=36°.
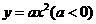 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点 ,两直角边与该抛物线交于
,两直角边与该抛物线交于 、
、 两点,请解答以下问题:
两点,请解答以下问题: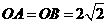 (如图1),求
(如图1),求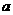 的值;
的值;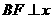 轴于点
轴于点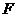 ,测得
,测得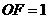 ,写出此时点
,写出此时点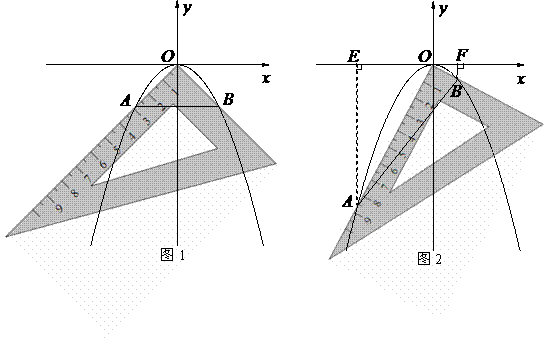
 ∵y轴和直线l都是⊙C的切线
∵y轴和直线l都是⊙C的切线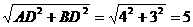
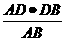 =
=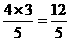
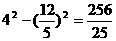
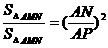 即
即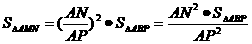 ……8分
……8分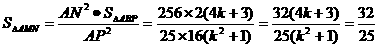
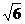 k2=2-
k2=2-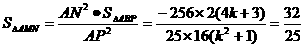
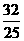 …10分
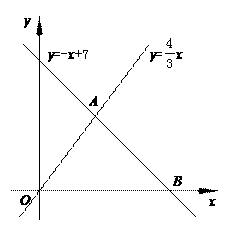
…10分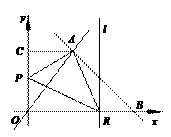 解:(1)根据题意,得,解得 ,∴A(3,4) .
解:(1)根据题意,得,解得 ,∴A(3,4) . 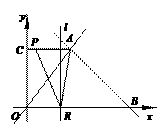 解之得t1=2,t2=6(舍)
解之得t1=2,t2=6(舍) 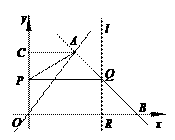 整理得,6t=24. ∴t=4(舍去)
整理得,6t=24. ∴t=4(舍去)
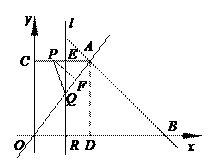 当AP=AQ时,7-t = (t-4),解得t = .
当AP=AQ时,7-t = (t-4),解得t = . 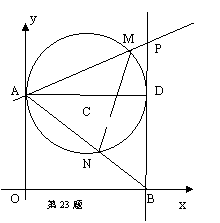 (3)是否存在使△AMN的面积等于
(3)是否存在使△AMN的面积等于 结论: HE=HF.
结论: HE=HF. 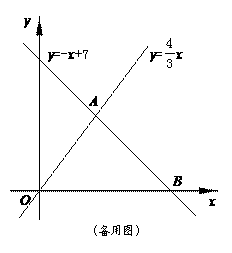
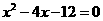 ,∴
,∴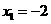 ,
,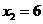 。
。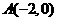 ,
,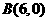 。····················1分
。····················1分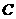 ,
,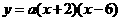 ,
,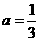 。
。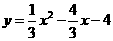 。········3分
。········3分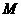 的坐标为(
的坐标为( ,0),过点
,0),过点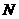 作
作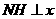 轴于点
轴于点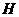 (如图(1))。
(如图(1))。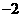 ,0),点
,0),点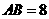 ,
,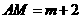 。···························4分
。···························4分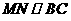 ,∴
,∴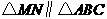 。
。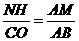 ,∴
,∴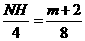 ,∴
,∴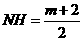 。·················5分
。·················5分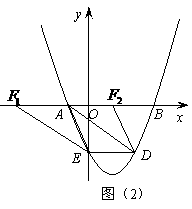 ∴
∴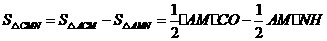
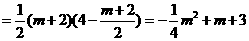 ······6分
······6分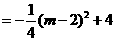 。
。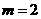 时,
时,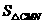 有最大值4。
有最大值4。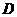 (4,
(4,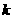 )在抛物线
)在抛物线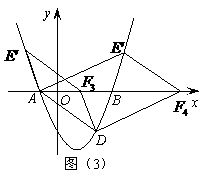 ∴当
∴当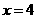 时,
时,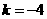 ,
, )。
)。 为平行四边形的边时,
为平行四边形的边时,

 ,
, (0,
(0,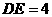 。
。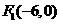 ,
,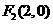 。 ··········9分
。 ··········9分 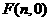 ,则平行四边形的对称中心为
,则平行四边形的对称中心为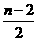 ,0)。·················10分
,0)。·················10分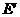 的坐标为(
的坐标为(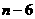 ,4)。
,4)。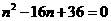 。
。 。
。 ,
, 。····
。····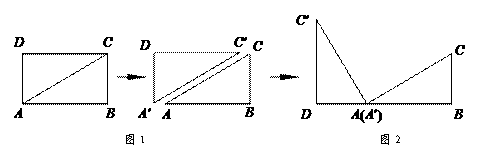 观察图2可知:与BC相等的线段是 ▲
,∠CAC′= ▲
°.
观察图2可知:与BC相等的线段是 ▲
,∠CAC′= ▲
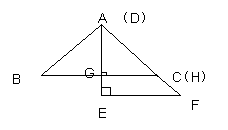
°.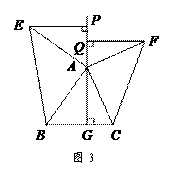 如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
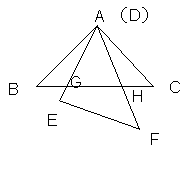
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.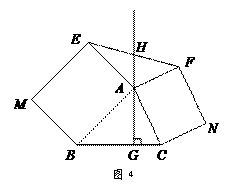 如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.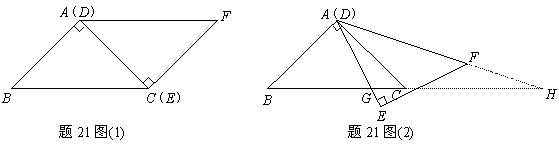
 )
)


 轴交于
轴交于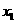 ,0)、
,0)、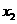 ,0)两点,且
,0)两点,且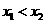 ,与
,与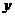 轴交于点
轴交于点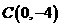 ,其中
,其中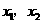 是方程
是方程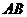 上的一个动点,过点
上的一个动点,过点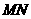 ∥
∥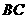 ,交
,交 于点
于点 ,当
,当 的面积最大时,求点
的面积最大时,求点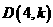 在(1)中抛物线上,点
在(1)中抛物线上,点 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点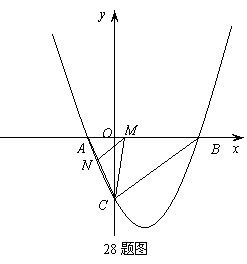

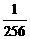
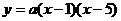 ,············1分
,············1分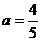 ,
,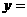
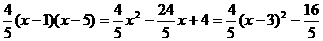 ,···········2分
,···········2分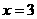 .······································3分
.······································3分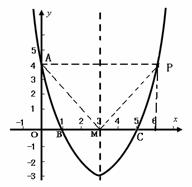 提示:由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3,又知点P的坐标中
提示:由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3,又知点P的坐标中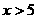 ,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,
,所以,MP>2,AP>2;因此以1、2、3、4为边或以2、3、4、5为边都不符合题意,所以四条边的长只能是3、4、5、6的一种情况,在Rt△AOM中,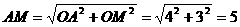 ,因为抛物线对称轴过点M,所以在抛物线
,因为抛物线对称轴过点M,所以在抛物线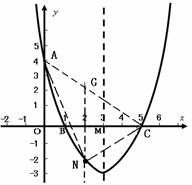 设N点的横坐标为
设N点的横坐标为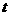 ,此时点N
,此时点N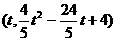 (
(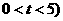 ,过点N作NG∥
,过点N作NG∥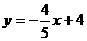 ;把
;把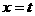 代入得:
代入得: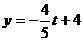 ,则G
,则G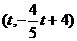 ,
,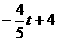 -(
-(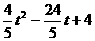 ),
), 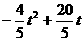 . ······································7分
. ······································7分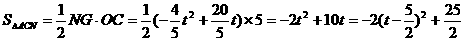
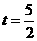 时,△CAN面积的最大值为
时,△CAN面积的最大值为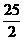 ,
,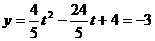 ,∴N(
,∴N(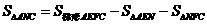
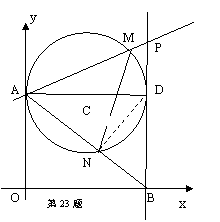
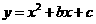 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.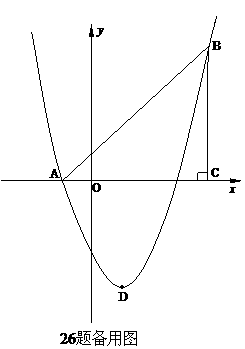
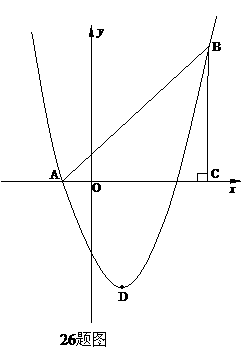
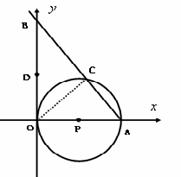 解:(1)解法一:连接OC,∵OA是⊙P的直径,∴OC⊥AB,
解:(1)解法一:连接OC,∵OA是⊙P的直径,∴OC⊥AB,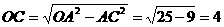 ,1分
,1分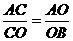 ,即
,即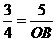 , ····················3分
, ····················3分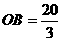 , ∴
, ∴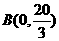 ····················4分
····················4分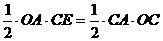 ,
,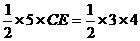 ,∴
,∴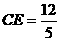 ,·························2分
,·························2分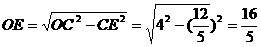 ∴
∴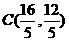 ,·········3分
,·········3分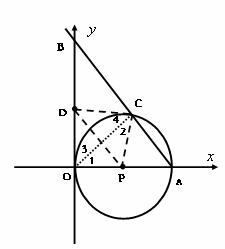 设经过A、C两点的直线解析式为:
设经过A、C两点的直线解析式为: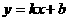 .
.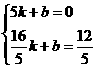 , 解得:
, 解得: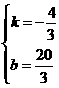 ,
,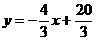 , ∴点
, ∴点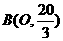 .·4分
.·4分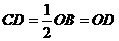 ,
,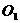 是DP的中点,圆心
是DP的中点,圆心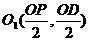 ,
,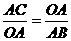 ,求得:AB=
,求得:AB=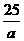 ,在Rt△ABO中,
,在Rt△ABO中,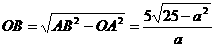 ,OD=
,OD=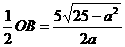 ,
,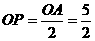
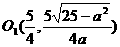 ,点
,点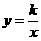 的图象上,
的图象上,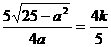 , ∴
, ∴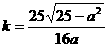
 . ················8分
. ················8分 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴
中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴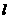 与
与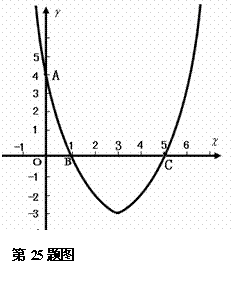 解:
解: