9. (2011福建泉州,24,9分)某电器商城“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
|
类别 |
冰箱 |
彩电 |
|
进价(元/台) |
2320 |
1900 |
|
售价(元/台) |
2420 |
1980 |
(1)按国家政策,农民购买“家电下乡”产品享受售价13℅的政府补贴。农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的补贴?
(2)为满足农民需求,商场决定用不超过85000元采购冰箱、彩电共40台,且冰箱的数量不少于彩电数量的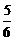 . 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?
. 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?
[答案]解:(1)(2420+1980)×13℅=572,...... .....................(3分)
(2)①设冰箱采购x台,则彩电采购(40-x)台,根据题意得
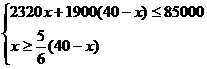
解不等式组得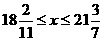 ,......
.................................(5分)
,......
.................................(5分)
因为x为整数,所以x = 19、20、21,
方案一:冰箱购买19台,彩电购买21台,
方案二:冰箱购买20台,彩电购买20台,
方案一:冰箱购买21台,彩电购买19台,
设商场获得总利润为y元,则
y =(2420-2320)x+(1980-1900)(40- x)...... .................(7分)
=20 x + 3200
∵20>0,
∴y随x的增大而增大,
∴当x =21时,y最大 = 20×21+3200 = 3620. ...... .......................(9分)
4. (2011山东日照,22,9分)某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(元)如下表:
|
|
空调机 |
电冰箱 |
|
甲连锁店 |
200 |
170 |
|
乙连锁店 |
160 |
150 |
设集团调配给甲连锁店x台空调机,集团卖出这100台电器的总利润为y(元).
(1)求y关于x的函数关系式,并求出x的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利a元销售,其他的销售利润不变,并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润,问该集团应该如何设计调配方案,使总利润达到最大?
[答案] (1)根据题意知,调配给甲连锁店电冰箱(70-x)台,
调配给乙连锁店空调机(40-x)台,电冰箱(x-10)台,
则y=200x+170(70-x)+160(40-x)+150(x-10),
即y=20x+16800.∵ 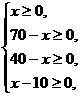
∴10≤x≤40.
∴y=20x+168009 (10≤x≤40);
(2)按题意知:y=(200-a)x+170(70-x)+160(40-x)+150(x-10),
即y=(20-a)x+16800.
∵200-a>170,∴a<30.
当0<a<20时,x=40,即调配给甲连锁店空调机40台,电冰箱30台,乙连锁店空调0台,电冰箱30台;
当a=20时,x的取值在10≤x≤40内的所有方案利润相同;
当20<a<30时,x=10,即调配给甲连锁店空调机10台,电冰箱60台,乙连锁店空调30台,电冰箱0台;
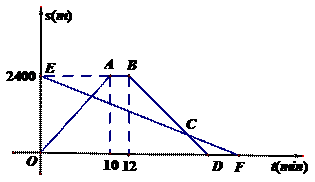
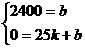 ,解得
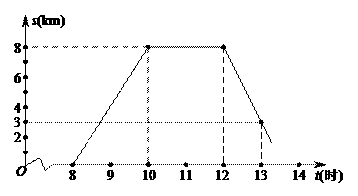
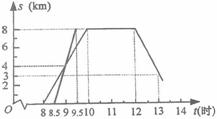
,解得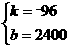 ,∴解析式为S2=-96t+2400.
,∴解析式为S2=-96t+2400.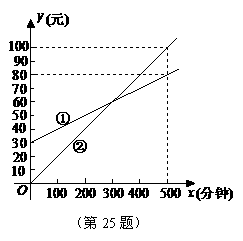

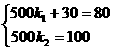 ,解得
,解得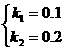
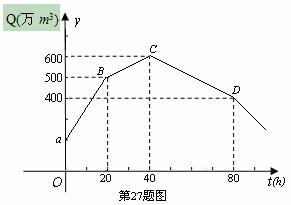
 吨,应交水费为y元,写出y与
吨,应交水费为y元,写出y与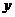 元.
元. 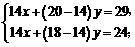
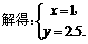
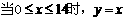 ;
;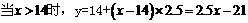 ,
, 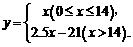
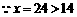 ,
,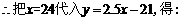
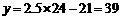 .
.
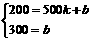 ,解得
,解得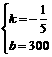
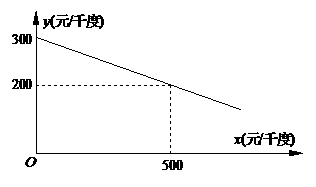
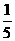 x+300(x≥0)
x+300(x≥0)