摘要：28．(1)∵.∴.. ∴..····················1分 又∵抛物线过点... 故设抛物线的解析式为. 将点的坐标代入.求得. ∴抛物线的解析式为.········3分 (2)设点的坐标为(.0).过点作轴于点. ∵点的坐标为(.0).点的坐标为(6.0). ∴..···························4分 ∵.∴. ∴.∴.∴.·················5分 ∴ ······6分 . ∴当时.有最大值4. 此时.点的坐标为(2.0).··············7分 (3)∵点(4.)在抛物线上. ∴当时.. ∴点的坐标是(4.). 如图(2).当为平行四边形的边时.. ∵(4.).∴(0.).. ∴.. ··········9分 ① 如图(3).当为平行四边形的对角线时. 设.则平行四边形的对称中心为 (.0).·················10分 ∴的坐标为(.4). 把(.4)代入.得. 解得 . ..···· 27． 情境观察 将矩形ABCD纸片沿对角线AC剪开.得到△ABC和△A′C′D.如图1所示.将△A′C′D的顶点A′与点A重合.并绕点A按逆时针方向旋转.使点D.A(A′).B在同一条直线上.如图2所示． 观察图2可知:与BC相等的线段是 ▲ .∠CAC′= ▲ °． 问题探究 如图3.△ABC中.AG⊥BC于点G.以A为直角顶点.分别以AB.AC为直角边.向△ABC外作等腰Rt△ABE和等腰Rt△ACF.过点E.F作射线GA的垂线.垂足分别为P.Q. 试探究EP与FQ之间的数量关系.并证明你的结论. 拓展延伸 如图4.△ABC中.AG⊥BC于点G.分别以AB.AC为一边向△ABC外作矩形ABME和矩形ACNF.射线GA交EF于点H. 若AB= k AE.AC= k AF.试探究HE与HF之间的数量关系.并说明理由.
网址：http://m.1010jiajiao.com/timu3_id_495306[举报]
已知平行于x轴的直线y=a（a≠0）与函数y=x和函数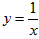
的图象分别交于点A和点B，又有定点P（2，0）。
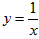的图象分别交于点A和点B，又有定点P（2，0）。
（1）若a>0，且tan∠POB=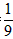
，求线段AB的长；
（2）在过A、B两点且顶点在直线y=x上的抛物线中，已知线段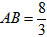
，且在它的对称轴左边时，y随着x的增大而增大，试求出满足条件的抛物线的解析式；
（3）已知经过A、B、P三点的抛物线，平移后能得到的图象，求点P到直线AB的距离。
查看习题详情和答案>>
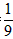，求线段AB的长；（2）在过A、B两点且顶点在直线y=x上的抛物线中，已知线段
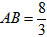，且在它的对称轴左边时，y随着x的增大而增大，试求出满足条件的抛物线的解析式；（3）已知经过A、B、P三点的抛物线，平移后能得到的图象，求点P到直线AB的距离。
在平面直角坐标系中，将直线l：y=-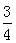
x-
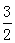沿x轴翻折，得到一条新直线，与x轴交于点A，与y轴交于点B，将抛物线C1：y=
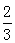x2沿x轴平移，得到一条新抛物线C2，与y轴交于点D，与直线AB交于点E、点F。
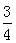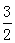x-沿x轴翻折，得到一条新直线，与x轴交于点A，与y轴交于点B，将抛物线C1：y=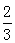x2沿x轴平移，得到一条新抛物线C2，与y轴交于点D，与直线AB交于点E、点F。
（l）求直线AB的解析式；
（2）若线段DF//x轴，求抛物线C2的解析式；
（3）在（2）的条件下，若点F在y轴右侧，过F作FH⊥x轴于点G，与直线l交于点H，一条直线m（m不过△AFH的顶点）与AF交于点M，与FH交于点N，如果直线m既平分△AFH的面积，又平分△AFH的周长，求直线m的解析式。
查看习题详情和答案>>
（2）若线段DF//x轴，求抛物线C2的解析式；
（3）在（2）的条件下，若点F在y轴右侧，过F作FH⊥x轴于点G，与直线l交于点H，一条直线m（m不过△AFH的顶点）与AF交于点M，与FH交于点N，如果直线m既平分△AFH的面积，又平分△AFH的周长，求直线m的解析式。
如图1，连接△ABC的各边中点得到一个新的△A1B1C1，又连接△A1B1C1的各边中点得到△A2B2C2，如此无限继续下去，得到一系列三角形：△ABC，△A1B1C1，△A2B2C2，…。已知A（0，0），B（3，0），C（2，2）。
（1）求这一系列三角形趋向于一个点M的坐标；
（2）如图2，分别求出经过A，B，C三点的抛物线解析式和经过A1，B1，C1三点的抛物线解析式；
（3）设两抛物线的交点分别为E、F，连接EF、EC1、FC1、EC2、FC2、C1C2，问：C2与△EC1F的关系是什么？（4）如图3，问：A，A2，C，C2四点可不可能在同一条抛物线上，试说明理由。
查看习题详情和答案>>
（2）如图2，分别求出经过A，B，C三点的抛物线解析式和经过A1，B1，C1三点的抛物线解析式；
（3）设两抛物线的交点分别为E、F，连接EF、EC1、FC1、EC2、FC2、C1C2，问：C2与△EC1F的关系是什么？（4）如图3，问：A，A2，C，C2四点可不可能在同一条抛物线上，试说明理由。
如图，已知抛物线
（1）求证：无论m取什么实数，这条抛物线与x轴一定有交点。
（2）设这条抛物线与x轴的正半轴交于
两点（设A点在B点的左侧），当线段AB长为3时，求这条抛物线的解析式，以及A、B两点的坐标。
（3）设（2）中的抛物线与y轴交于点C，过A、B两点分别作两条直线与x轴垂直，又过点C作直线l，l与这两条直线依次交于x轴上方的E、F两点，如果梯形ABFE的面积等于9，求直线l的解析式。
（4）设线段AB上有一个动点P，P从A点出发向B点移动（但不与B重合），过P点作PM垂直x轴，交（2）中的抛物线于点M。设
，问：是否存在这样的t值，使
与以P、M、B为顶点的直角三角形相似？如果存在，求出t的值；如果不存在，请说明理由。
查看习题详情和答案>>
（2）设这条抛物线与x轴的正半轴交于
两点（设A点在B点的左侧），当线段AB长为3时，求这条抛物线的解析式，以及A、B两点的坐标。（3）设（2）中的抛物线与y轴交于点C，过A、B两点分别作两条直线与x轴垂直，又过点C作直线l，l与这两条直线依次交于x轴上方的E、F两点，如果梯形ABFE的面积等于9，求直线l的解析式。
（4）设线段AB上有一个动点P，P从A点出发向B点移动（但不与B重合），过P点作PM垂直x轴，交（2）中的抛物线于点M。设
，问：是否存在这样的t值，使与以P、M、B为顶点的直角三角形相似？如果存在，求出t的值；如果不存在，请说明理由。