摘要: 解: B(4.5)------------1分 ∵二次函数的图像经过点A ∴ ------------2分 解得:b=-2 c=-3 ------------3分 (2如26题图:∵直线AB经过点A ∴直线AB的解析式为:y=x+1 ∵二次函数 ∴设点E(t. t+1),则F(t.) ------------4分 ∴EF= ------------5分 = ∴当时.EF的最大值= ∴点E的坐标为(.) ------------------------6分 (3)①如26题图:顺次连接点E.B.F.D得四边形EBFD. 可求出点F的坐标(.),点D的坐标为 S = S + S = 26题备用图 = -----------------------------------9分 ②如26题备用图:ⅰ)过点E作a⊥EF交抛物线于点P,设点P(m,) 则有: 解得:, ∴, ⅱ)过点F作b⊥EF交抛物线于.设(n.) 则有: 解得: .∴ 综上所述:所有点P的坐标:.(. 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分 26.如图.在平面直角坐标系中.O为坐标原点.P是反比例函数y=(x>0)图象上的任意一点.以P为圆心.PO为半径的圆与x.y轴分别交于点A.B. (1)判断P是否在线段AB上.并说明理由, (2)求△AOB的面积, (3)Q是反比例函数y=(x>0)图象上异于点P的另一点.请以Q为圆心.QO 半径画圆与x.y轴分别交于点M.N.连接AN.MB.求证:AN∥MB. 解:(1)点P在线段AB上.理由如下: ∵点O在⊙P上.且∠AOB=90° ∴AB是⊙P的直径 ∴点P在线段AB上. (2)过点P作PP1⊥x轴.PP2⊥y轴.由题意可知PP1.PP2 是△AOB的中位线.故S△AOB=OA×OB=×2 PP1×PP2 ∵P是反比例函数y=(x>0)图象上的任意一点 ∴S△AOB=OA×OB=×2 PP1×2PP2=2 PP1×PP2=12. (3)如图.连接MN.则MN过点Q.且S△MON=S△AOB=12. ∴OA·OB=OM·ON ∴ ∵∠AON=∠MOB ∴△AON∽△MOB ∴∠OAN=∠OMB ∴AN∥MB. 27.如图.在边长为2的正方形ABCD中.P为AB的中点.Q为边CD上一动点.设DQ=t(0≤t≤2).线段PQ的垂直平分线分别交边AD.BC于点M.N.过Q作QE⊥AB于点E.过M作MF⊥BC于点F. (1)当t≠1时.求证:△PEQ≌△NFM, (2)顺次连接P.M.Q.N.设四边形PMQN的面积为S.求出S与自变量t之间的函数关系式.并求S的最小值. 解:(1)∵四边形ABCD是正方形 ∴∠A=∠B=∠D=90°.AD=AB ∵QE⊥AB.MF⊥BC ∴∠AEQ=∠MFB=90° ∴四边形ABFM.AEQD都是矩形 ∴MF=AB.QE=AD.MF⊥QE 又∵PQ⊥MN ∴∠EQP=∠FMN 又∵∠QEP=∠MFN=90° ∴△PEQ≌△NFM. (2)∵点P是边AB的中点.AB=2.DQ=AE=t ∴PA=1.PE=1-t.QE=2 由勾股定理.得PQ== ∵△PEQ≌△NFM ∴MN=PQ= 又∵PQ⊥MN ∴S===t2-t+ ∵0≤t≤2 ∴当t=1时.S最小值=2. 综上:S=t2-t+.S的最小值为2. 28.如图.在Rt△ABC中.∠B=90°.AB=1.BC=.以点C为圆心.CB为半径的弧交CA于点D,以点A为圆心.AD为半径的弧交AB于点E. (1)求AE的长度, (2)分别以点A.E为圆心.AB长为半径画弧.两弧交于点F(F与C在AB两侧).连接AF.EF.设EF交弧DE所在的圆于点G.连接AG.试猜想∠EAG的大小.并说明理由. 解:(1)在Rt△ABC中.由AB=1.BC=得 AC== ∵BC=CD.AE=AD ∴AE=AC-AD=. (2)∠EAG=36°.理由如下: ∵FA=FE=AB=1.AE= ∴= ∴△FAE是黄金三角形 ∴∠F=36°.∠AEF=72° ∵AE=AG.FA=FE ∴∠FAE=∠FEA=∠AGE ∴△AEG∽△FEA ∴∠EAG=∠F=36°.
网址:http://m.1010jiajiao.com/timu3_id_495303[举报]
已知:在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,点A在点B的左侧,若抛物线的对称轴为x=1,点A的坐标为(-1,0).
(1)求这个二次函数的解析式;
(2)设抛物线的顶点为C,抛物线上一点D的坐标为(-3,12),过点B、D的直线与抛物线的对称轴交于点E.问:是否存在这样的点F,使得以点B、C、E、F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若在BD上存在一点P,使得直线AP将四边形ACBD分成了面积相等的两部分,请你求出此时点P的坐标. 查看习题详情和答案>>
(1)求这个二次函数的解析式;
(2)设抛物线的顶点为C,抛物线上一点D的坐标为(-3,12),过点B、D的直线与抛物线的对称轴交于点E.问:是否存在这样的点F,使得以点B、C、E、F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若在BD上存在一点P,使得直线AP将四边形ACBD分成了面积相等的两部分,请你求出此时点P的坐标. 查看习题详情和答案>>
 已知:将函数y=
已知:将函数y=
| ||
| 3 |
(1)写出这个新的函数的解析式;
(2)若平移前后的这两个函数图象分别与y轴交于O,A两点,与直线x=-
| 3 |
(3)若(2)中的四边形(不包括边界)始终覆盖着二次函数y=x2-2bx+b2+
| 1 |
| 2 |
 已知一次函数y1=kx+b(k≠0)的图象与反比例函数
已知一次函数y1=kx+b(k≠0)的图象与反比例函数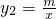 (m≠0)的图象交于A(-2,1)、B(1,n)两点.
(m≠0)的图象交于A(-2,1)、B(1,n)两点.