摘要:解:(1)解法一:连接OC.∵OA是⊙P的直径.∴OC⊥AB. 在Rt△AOC中..1分 在 Rt△AOC和Rt△ABO中.∵∠CAO=∠OAB ∴Rt△AOC∽Rt△ABO.····························2分 ∴.即. ····················3分 ∴ . ∴····················4分 解法二:连接OC.因为OA是⊙P的直径. ∴∠ACO=90° 在Rt△AOC中.AO=5.AC=3.∴OC=4. ············1分 过C作CE⊥OA于点E.则:. 即:.∴.·························2分 ∴ ∴.·········3分 设经过A.C两点的直线解析式为:. 把点A(5.0).代入上式得: . 解得:. ∴ . ∴点 .·4分 (2)点O.P.C.D四点在同一个圆上.理由如下: 连接CP.CD.DP.∵OC⊥AB.D为OB上的中点. ∴. ∴∠3=∠4.又∵OP=CP.∴∠1=∠2.∴∠1+∠3=∠2+∠4=90°. ∴PC ⊥CD.又∵DO⊥OP.∴Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形.∴PD上的中点到点O.P.C.D四点的距离相等. ∴点O.P.C.D在以DP为直径的同一个圆上, ·················6分 由上可知.经过点O.P.C.D的圆心是DP的中点.圆心. 由(1)知:Rt△AOC∽Rt△ABO.∴.求得:AB=.在Rt△ABO中. .OD=. ∴.点在函数的图象上. ∴. ∴. ················8分 如图.在平面直角坐标系中.已知抛物线经过点A.抛物线对称轴与轴相交于点M. (1)求抛物线的解析式和对称轴, (2)设点P为抛物线()上的一点.若以A.O.M.P为顶点的四边形四条边的长度为四个连续的正整数.请你直接写出点P的坐标, (3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N.使△NAC的面积最大?若存在.请你求出点N的坐标,若不存在.请你说明理由. 解:
网址:http://m.1010jiajiao.com/timu3_id_495301[举报]
 (1)我们知道三角形的内角和是180°,请猜测四边形的内角和是多少度?
(1)我们知道三角形的内角和是180°,请猜测四边形的内角和是多少度?解:四边形的四个内角和等于
360
360
°(2)利用下面两种方法验证你的猜想,请说明理由:
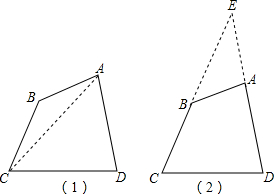
解法一:如图1,连接四边形ABCD的对角线AC.
解法二:如图2,延长CB、DA相交于点E.
 (1)我们知道三角形的内角和是180°,请猜测四边形的内角和是多少度?
(1)我们知道三角形的内角和是180°,请猜测四边形的内角和是多少度?
解:四边形的四个内角和等于______°
(2)利用下面两种方法验证你的猜想,请说明理由:
解法一:如图1,连接四边形ABCD的对角线AC.
解法二:如图2,延长CB、DA相交于点E.
查看习题详情和答案>>
用代入法解方程组
有以下步骤:
①:由(1),得y=
(3);
②:由(3)代入(1),得7x-2×
=3;
③:整理得3=3;
④:∴x可取一切有理数,原方程组有无数个解
以上解法,造成错误的一步是( )
|
①:由(1),得y=
| 7x-3 |
| 2 |
②:由(3)代入(1),得7x-2×
| 7x-3 |
| 2 |
③:整理得3=3;
④:∴x可取一切有理数,原方程组有无数个解
以上解法,造成错误的一步是( )
| A、① | B、② | C、③ | D、④ |
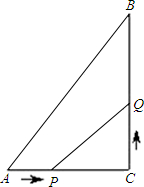 匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,点P,Q分另从起点同时出发,移动到某一位置时所需时间为t秒.
匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,点P,Q分另从起点同时出发,移动到某一位置时所需时间为t秒.