0 49386 49394 49400 49404 49410 49412 49416 49422 49424 49430 49436 49440 49442 49446 49452 49454 49460 49464 49466 49470 49472 49476 49478 49480 49481 49482 49484 49485 49486 49488 49490 49494 49496 49500 49502 49506 49512 49514 49520 49524 49526 49530 49536 49542 49544 49550 49554 49556 49562 49566 49572 49580 447348
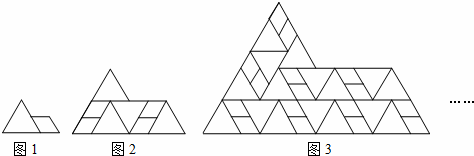
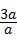 =3
=3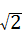 x,则正方形的周率是a2=
x,则正方形的周率是a2=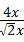 =2
=2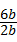 =3,
=3,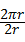 =π,
=π,
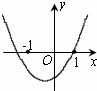
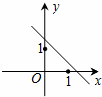 B、
B、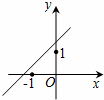
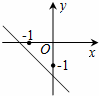 D、
D、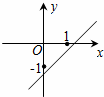

 )×(﹣2)=1
)×(﹣2)=1 中,把抛物线
中,把抛物线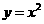 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线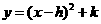 .所得抛物线与
.所得抛物线与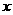 轴交于
轴交于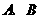 两点(点
两点(点 在点
在点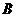 的左边),与
的左边),与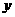 轴交于点
轴交于点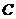 ,顶点为
,顶点为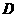 .
.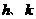 的值;
的值; 的形状,并说明理由;
的形状,并说明理由;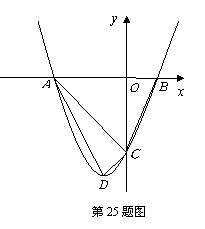 (3)在线段
(3)在线段 上是否存在点
上是否存在点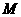 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点 如图,直角梯形ABCD中,AD∥BC,∠A=90°,
如图,直角梯形ABCD中,AD∥BC,∠A=90°,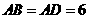 ,
,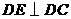 交AB于E,DF平分∠EDC交BC于F,连结EF.
交AB于E,DF平分∠EDC交BC于F,连结EF.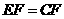 ;
;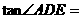
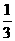 时,求EF的长.
时,求EF的长.