0 49414 49422 49428 49432 49438 49440 49444 49450 49452 49458 49464 49468 49470 49474 49480 49482 49488 49492 49494 49498 49500 49504 49506 49508 49509 49510 49512 49513 49514 49516 49518 49522 49524 49528 49530 49534 49540 49542 49548 49552 49554 49558 49564 49570 49572 49578 49582 49584 49590 49594 49600 49608 447348
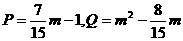 (m为任意实数),则P、Q的大小关系为( )
(m为任意实数),则P、Q的大小关系为( )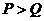 B.
B. 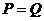 C.
C. 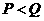 D.不能确定
D.不能确定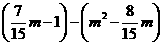 =
=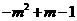 =
=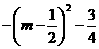 <0,故P<Q.
<0,故P<Q.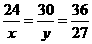 ①或
①或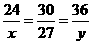 ②(注:27cm不可能是最小边),由①解得x=18,y=22.5,符合题意;由②解得x=
②(注:27cm不可能是最小边),由①解得x=18,y=22.5,符合题意;由②解得x=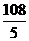 ,y=
,y=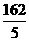 ,x+ y=
,x+ y=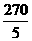 =54>45,不合题意,舍去.
=54>45,不合题意,舍去.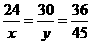 (注:只能是45是最大边),解得x=30,y=
(注:只能是45是最大边),解得x=30,y=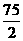 ,x+ y=30+37.5=67.5>27,不合题意,舍去.
,x+ y=30+37.5=67.5>27,不合题意,舍去.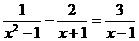 的解是
的解是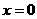 ;④如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.其中真命题的个数有( )
;④如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.其中真命题的个数有( )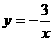 B.
B. 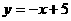 C.
C. 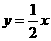 D.
D. 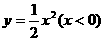
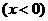 ,y随x增大而减小,舍去.故选C.
,y随x增大而减小,舍去.故选C.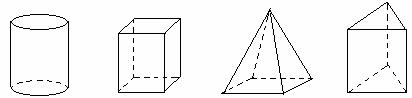
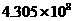 亩 B.
亩 B. 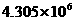 亩 C.
亩 C. 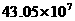 亩 D.
亩 D. 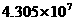 亩
亩 的形式(其中1≤
的形式(其中1≤ <10,n为整数,这种计数法称为科学记数法.科学记数法是每年中考试卷中的必考问题,应掌握:⑴表达形式为:
<10,n为整数,这种计数法称为科学记数法.科学记数法是每年中考试卷中的必考问题,应掌握:⑴表达形式为: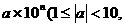 n表示小数点移动的位数).科学记数法可以表示绝对值大于10的数,也可以表示绝对值小于1的数.⑵当表示绝对值大于10的数时应注意:小数点向左移到第一位数字后,看小数点移动了几位,n的值就是几,表达式中的n是应为正整数.⑶当表示绝对值小于1的数时应注意:小数点向右移到第一位不为零的数后,看小数点移动了几位,n的值就是几,表达式中的n应为负整数.
n表示小数点移动的位数).科学记数法可以表示绝对值大于10的数,也可以表示绝对值小于1的数.⑵当表示绝对值大于10的数时应注意:小数点向左移到第一位数字后,看小数点移动了几位,n的值就是几,表达式中的n是应为正整数.⑶当表示绝对值小于1的数时应注意:小数点向右移到第一位不为零的数后,看小数点移动了几位,n的值就是几,表达式中的n应为负整数.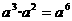 B.
B. 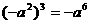 C.
C. 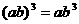 D.
D.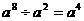
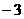 的倒数为( )
的倒数为( )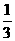 C.
C.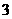 D.
D. 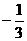
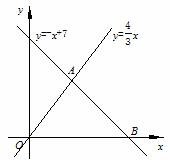 (本题满分12分)如图,已知一次函数y = -
x +7与正比例函数y = x的图象交于点A,
(本题满分12分)如图,已知一次函数y = -
x +7与正比例函数y = x的图象交于点A,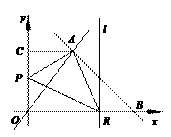 存在,请说明理由.
存在,请说明理由.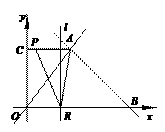 (3+7)×4-×3×(4-t)- t(7-t)-
t×4=8
(3+7)×4-×3×(4-t)- t(7-t)-
t×4=8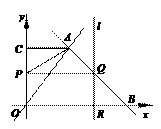 当P在CA上运动时,4≤t<7. 此时直线l交AO于Q。过A作AD⊥OB于D,则AD=BD=4.
当P在CA上运动时,4≤t<7. 此时直线l交AO于Q。过A作AD⊥OB于D,则AD=BD=4.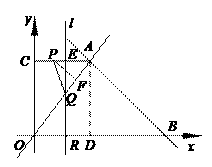 当AP=AQ时,7-t = (t-4),解得t = .
当AP=AQ时,7-t = (t-4),解得t = .
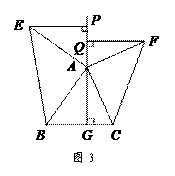
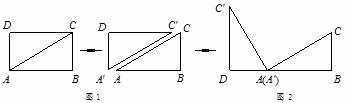 (本题满分12分)情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是
▲ ,∠CAC′= ▲
°.问题探究如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
(本题满分12分)情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是
▲ ,∠CAC′= ▲
°.问题探究如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.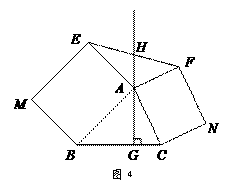 拓展延伸如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
[答案]解:情境观察
拓展延伸如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
[答案]解:情境观察 结论: HE=HF.
结论: HE=HF.