摘要：21．.△ABC与△EFD为等腰直角三角形.AC与DE重合.AB=AC=EF=9.∠BAC=∠DEF=90º.固定△ABC.将△DEF绕点A顺时针旋转.当DF边与AB边重合时.旋转中止．现不考虑旋转开始和结束时重合的情况.设DE.DF分别交BC 于G.H点.如图(2) (1)问:始终与△AGC相似的三角形有 及 , (2)设CG=x.BH=y.求y关于x的函数关系式的情形说明理由) (3)问:当x为何值时.△AGH是等腰三角形. (1).△HAB △HGA, (2).由△AGC∽△HAB.得AC/HB=GC/AB.即9/y=x/9.故y=81/x (0<x<) (3)因为:∠GAH= 45° ①当∠GAH= 45°是等腰三角形.的底角时.如图(1):可知CG=x=/2 ②当∠GAH= 45°是等腰三角形.的顶角时, 如图(2):由△HGA∽△HAB 知:HB= AB=9.也可知BG=HC.可得:CG=x=18- 图 如图.抛物线与轴交于(.0).(.0)两点.且.与轴交于点.其中是方程的两个根. (1)求抛物线的解析式, (2)点是线段上的一个动点.过点作∥.交于点.连接.当的面积最大时.求点的坐标, (3)点在(1)中抛物线上.点为抛物线上一动点.在轴上是否存在点.使以为顶点的四边形是平行四边形.如果存在.求出所有满足条件的点的坐标.若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_495305[举报]
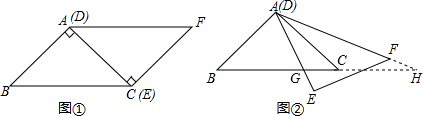
如图①，△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=AC=EF=9，∠BAC=∠DEF=90°．如图②所示，现固定△ABC，将△EFD绕点A顺时针旋转，当AE边与AB边重合时，旋转中止，若不考虑旋转开始和结束时这两种特殊的情形，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H两点，设CG=x．
（1）始终与△AGC相似的三角形有
（2）设BH=y，求y关于x的函数关系式；
（3）当x为何值时，△AGH是等腰三角形？
查看习题详情和答案>>
（1）始终与△AGC相似的三角形有
△HAB
△HAB
及△HGA
△HGA
；（2）设BH=y，求y关于x的函数关系式；
（3）当x为何值时，△AGH是等腰三角形？
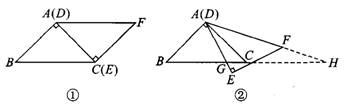
如图①，△ABC与△EFD为等腰直角三角形，AC与DE重合，AB＝EF＝9，∠BAC＝∠DEF＝90°，固定△ABC，将△EFD绕点A顺时针旋转，当DF边与AB边重合时，旋转中止，不考虑旋转开始和结束时重合的情况，设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点，如图②
【小题1】问：始终与△AGC相似的三角形有_______及_______
【小题2】设CG＝x，BH＝y，求y关于x的函数关系式（只要求根据2的情况说明理由）
【小题3】问：当x为何值时，△AGH是等腰三角形？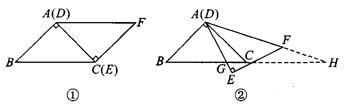
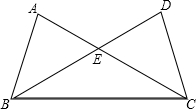（2013•舟山）如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．