摘要:解:情境观察 AD(或A′D).90 问题探究 结论:EP=FQ. 证明:∵△ABE是等腰三角形.∴AB=AE.∠BAE=90°. ∴∠BAG+∠EAP=90°.∵AG⊥BC.∴∠BAG+∠ABG=90°.∴∠ABG=∠EAP. ∵EP⊥AG.∴∠AGB=∠EPA=90°.∴Rt△ABG≌Rt△EAP. ∴AG=EP. 同理AG=FQ. ∴EP=FQ. 拓展延伸 结论: HE=HF. 理由:过点E作EP⊥GA.FQ⊥GA.垂足分别为P.Q. ∵四边形ABME是矩形.∴∠BAE=90°. ∴∠BAG+∠EAP=90°.AG⊥BC.∴∠BAG+∠ABG=90°. ∴∠ABG=∠EAP. ∵∠AGB=∠EPA=90°.∴△ABG∽△EAP.∴ = . 同理△ACG∽△FAQ.∴ = . ∵AB= k AE.AC= k AF.∴ = = k.∴ = . ∴EP=FQ. ∵∠EHP=∠FHQ.∴Rt△EPH≌Rt△FQH. ∴HE=HF 28.如图.已知一次函数y = - x +7与正比例函数y = x的图象交于点A.且与x轴交于点B. (1)求点A和点B的坐标, (2)过点A作AC⊥y轴于点C.过点B作直线l∥y轴.动点P从点O出发.以每秒1个单位长的速度.沿O-C-A的路线向点A运动,同时直线l从点B出发.以相同速度向左平移.在平移过程中.直线l交x轴于点R.交线段BA或线段AO于点Q.当点P到达点A时.点P和直线l都停止运动.在运动过程中.设动点P运动的时间为t秒. ①当t为何值时.以A.P.R为顶点的三角形的面积为8? ②是否存在以A.P.Q为顶点的三角形是等腰三角形?若存在.求t的值,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_495307[举报]
27、情境观察
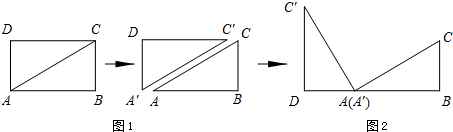
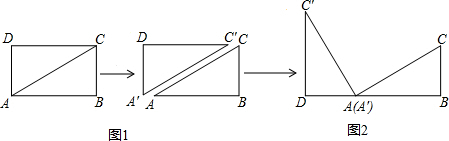
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是
问题探究
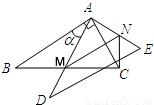
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.

拓展延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.

查看习题详情和答案>>
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是
AD
,∠CAC′=90
°.
问题探究
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.

拓展延伸
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.

情境观察
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是

问题探究
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.

查看习题详情和答案>>
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是
AD或A′D
AD或A′D
,∠CAC′=90
90
°.
问题探究
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.

情境·观察:
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△ ,如图1所示,将△
,如图1所示,将△ 的顶点
的顶点 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A( ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角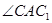 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。
问题·探究:
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。

关系·拓展:
如图4,已知正方形ABCD,P为边BC上任意一点,连结AP,把AP绕点P顺时针方向旋转90°,点A对应点为点 ,连接
,连接 ,求
,求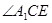 的度数。
的度数。
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△
 ,如图1所示,将△
,如图1所示,将△ 的顶点
的顶点 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A( ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角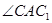 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。
问题·探究:
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q,试探究EP与FQ之间的数量关系,并证明你的结论。

关系·拓展:
如图4,已知正方形ABCD,P为边BC上任意一点,连结AP,把AP绕点P顺时针方向旋转90°,点A对应点为点
 ,连接
,连接 ,求
,求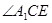 的度数。
的度数。 S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.
S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.
 S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.
S△ABC时,试判断直线AD与⊙N的位置关系,并说明理由.