24、(本题12分)
 已知两直线
已知两直线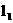 ,
,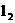 分别经过点A(1,0),点B
分别经过点A(1,0),点B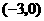 ,
,
并且当两直线同时相交于y正半轴的点C时,恰好有
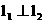 ,经过点A、B、C的抛物线的对称轴与直线
,经过点A、B、C的抛物线的对称轴与直线
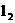 交于点K,如图所示。
交于点K,如图所示。
(1)求点C的坐标,并求出抛物线的函数解析式;
|
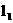 ,抛物线,直线
,抛物线,直线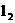 和x轴
和x轴
依次截得三条线段,问这三条线段有何数量关系?请说明理由。
(3)当直线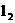 绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标。
24.解:
(1)设线段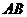 与
与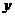 轴的交点为
轴的交点为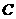 ,由抛物线的对称性可得
,由抛物线的对称性可得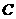 为
为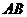 中点,
中点,

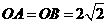 ,
,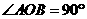 ,
,

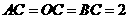 ,
,
 (
(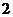 ,
,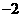 )
……… 2分
)
……… 2分
将 (
(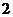 ,
,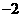 )代入抛物线
)代入抛物线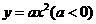 得,
得,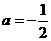 .
……… 3分
.
……… 3分
(2)解法一:过点 作
作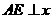 轴于点
轴于点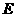 ,
,
 点
点 的横坐标为
的横坐标为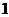 ,
,
 (1,
(1,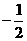 ),
……… 4分
),
……… 4分

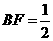 . 又
. 又
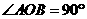 ,易知
,易知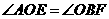 ,又
,又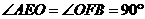 ,
,
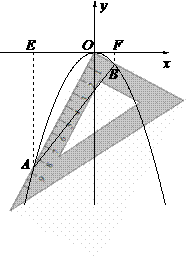
 △
△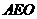 ∽△
∽△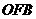 ,
,
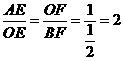

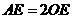 ……… 5分
……… 5分
设点 (
(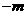 ,
,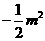 )(
)(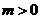 ),则
),则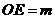 ,
,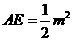 ,
,
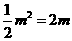

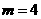 ,即点
,即点 的横坐标为
的横坐标为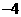 . ……… 6分
. ……… 6分
解法二:过点 作
作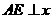 轴于点
轴于点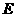 ,
,
 点
点 的横坐标为
的横坐标为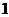 ,
,
 (1,
(1,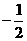 ),
……… 4分
),
……… 4分

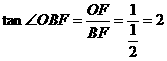

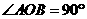 ,易知
,易知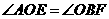 ,
,

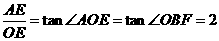 ,
,
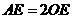 ……… 5分
……… 5分
设点 (-
(- ,
,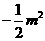 )(
)(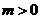 ),则
),则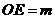 ,
,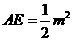 ,
,
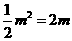

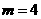 ,即点
,即点 的横坐标为
的横坐标为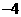 .
……… 6分
.
……… 6分
解法三:过点 作
作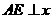 轴于点
轴于点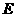 ,
,
 点
点 的横坐标为
的横坐标为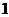 ,
,
 (1,
(1,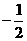 ),
……… 4分
),
……… 4分
设 (-
(- ,
,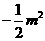 )(
)(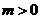 ),则
),则
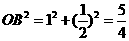 ,
,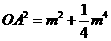 ,
,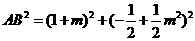 ,
,

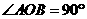

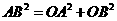 ,
,

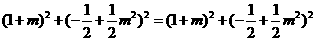 ,
,
解得: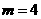 ,即点
,即点 的横坐标为
的横坐标为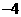 .
……… 6分
.
……… 6分
(3)解法一:设 (
(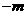 ,
,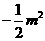 )(
)(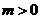 ),
), (
(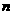 ,
,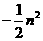 )(
)(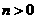 ),
),
设直线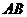 的解析式为:
的解析式为: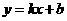 , 则
, 则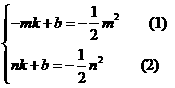 ,……… 7分
,……… 7分
 得,
得,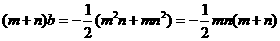 ,
,

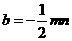 ……… 8分
……… 8分
又易知△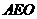 ∽△
∽△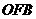 ,
,
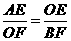 ,
,
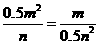 ,
,
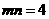 ……… 9分
……… 9分

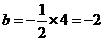 .由此可知不论
.由此可知不论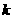 为何值,直线
为何值,直线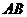 恒过点(
恒过点( ,
,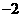 )………10分
)………10分
(说明:写出定点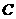 的坐标就给2分)
的坐标就给2分)
解法二:设 (
(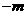 ,
,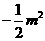 )(
)(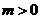 ),
), (
(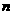 ,
,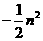 )(
)(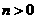 ),
),
直线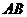 与
与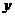 轴的交点为
轴的交点为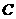 ,根据
,根据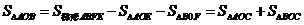 ,可得
,可得
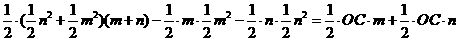 ,
,
化简,得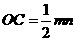 . ……… 8分
. ……… 8分
又易知△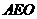 ∽△
∽△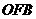 ,
,
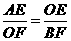 ,
,
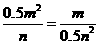 ,
,
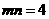 ……… 9分
……… 9分
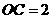 为固定值.故直线
为固定值.故直线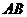 恒过其与
恒过其与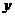 轴的交点
轴的交点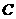 (
( ,
,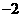 )……… 10分
)……… 10分
说明: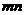 的值也可以通过以下方法求得.
的值也可以通过以下方法求得.
由前可知,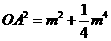 ,
,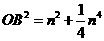 ,
,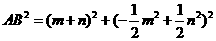 ,
,
由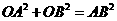 ,得:
,得: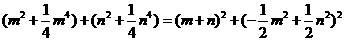 ,
,
化简,得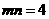 .
.
本答案仅供参考,若有其他解法,请参照本评分标准
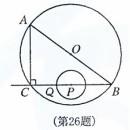
(南京市2011年)26.(8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由;
⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.


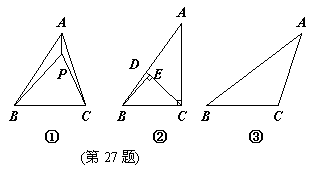
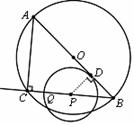
27.(9分)如图①,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
⑴如图②,已知Rt△ABC中,∠ACB=90°,∠ACB>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,试说明E是△ABC的自相似点.
⑵在△ABC中,∠A<∠B<∠C.
①如图③,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.

28.(11分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为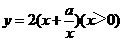 .
.
探索研究
 ⑴我们可以借鉴以前研究函数的经验,先探索函数
⑴我们可以借鉴以前研究函数的经验,先探索函数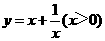 的图象性质.
的图象性质.
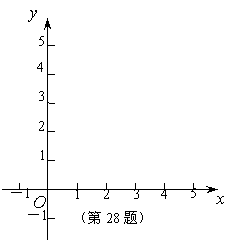
① 填写下表,画出函数的图象:
②
|
x |
…… |
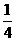 |
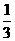 |
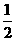 |
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数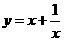 (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
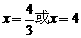 时,△PQW为直角三角形;
时,△PQW为直角三角形;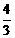 ,
,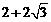
 (3)问当x为何值时,线段MN最短?求此时MN的值。
(3)问当x为何值时,线段MN最短?求此时MN的值。
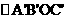 由
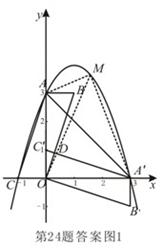
由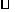 ABOC旋转得到,且点A的坐标为(0,3),
ABOC旋转得到,且点A的坐标为(0,3),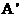 的坐标为(3,0)。
的坐标为(3,0)。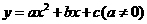 ,可得
,可得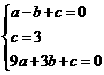 解得
解得
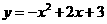 。
。 ∴
∴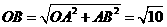 ,又
,又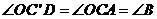 .
.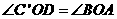 ,∴
,∴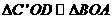 又
又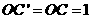 ,
,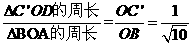 ,又△ABO的周长为
,又△ABO的周长为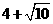 。
。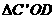 的周长为
的周长为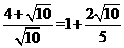 。
。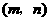 ,
,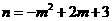 。
。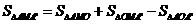
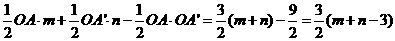
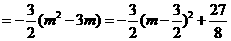
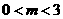 ,所以当
,所以当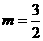 时,
时,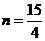 。△AMA’的面积有最大值
。△AMA’的面积有最大值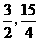 )时,△AMA’的面积有最大值,且最大值为
)时,△AMA’的面积有最大值,且最大值为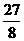 。
。 ,∴
,∴ ,
, 。
。 ,
,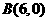 。·························1分
。·························1分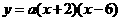 ,将点
,将点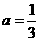 。
。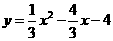 。················3分
。················3分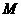 的坐标为(
的坐标为(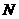 作
作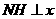 轴于点
轴于点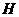 (如图(1))。
(如图(1))。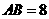 ,
,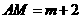 。···························4分
。···························4分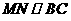 ,∴
,∴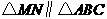 。
。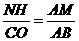 ,∴
,∴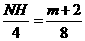 ,∴
,∴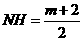 。·················5分
。·················5分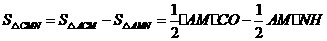
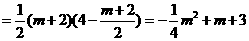 ···························6分
···························6分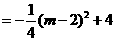 。
。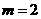 时,
时,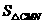 有最大值4。
有最大值4。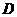 (4,
(4,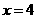 时,
时,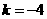 ,
,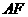 为平行四边形的边时,
为平行四边形的边时,

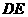 ,
,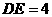 。
。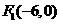 ,
,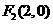 。 ···························9分
。 ···························9分 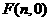 ,
,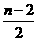 ,0)。 ··················10分
,0)。 ··················10分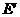 的坐标为(
的坐标为(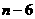 ,4)。
,4)。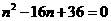 。
。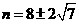 。
。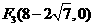 ,
,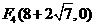 。·························12分
。·························12分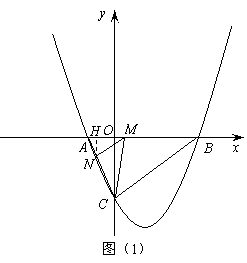
 ,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形
,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形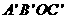 。
。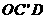 的周长;
的周长; 的面积最大?最大面积是多少?并求出此时点M的坐标。
的面积最大?最大面积是多少?并求出此时点M的坐标。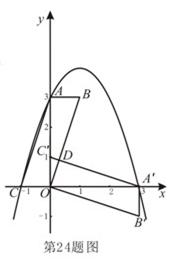
 ,即
,即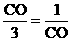
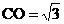
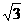 )
)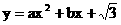
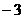 ,0)的坐标分别代入
,0)的坐标分别代入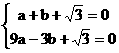
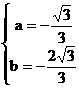
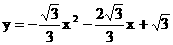
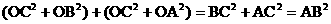
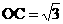
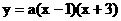 ,把C(0,
,把C(0,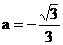
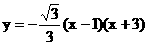
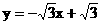 ,直线
,直线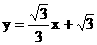
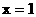
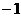 ,
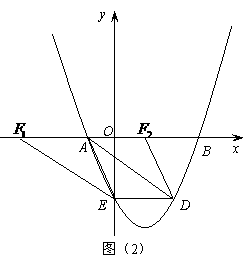
,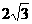 ),点D的坐标为(
),点D的坐标为(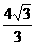 ),点E的坐标为(
),点E的坐标为(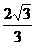 ),点F的坐标为(
),点F的坐标为(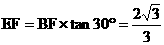 ,
,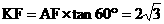 ,
,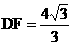
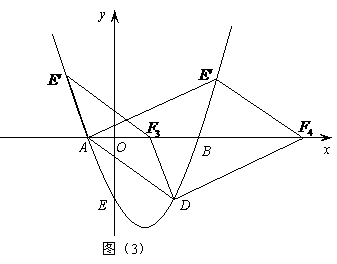
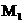 ,由抛物线对称性可知点
,由抛物线对称性可知点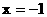 的对称点
的对称点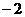 ,
, 为等腰三角形
为等腰三角形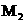 即点D坐标为(
即点D坐标为(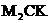 为等腰三角形;
为等腰三角形;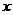 轴交于
轴交于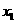 ,0)、
,0)、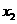 ,0)两点,且
,0)两点,且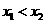 ,与
,与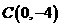 ,其中
,其中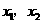 是方程
是方程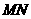 ∥
∥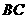 ,交
,交 于点
于点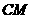 ,当
,当 的面积最大时,求点
的面积最大时,求点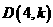 在(1)中抛物线上,点
在(1)中抛物线上,点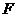 ,使以
,使以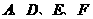 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点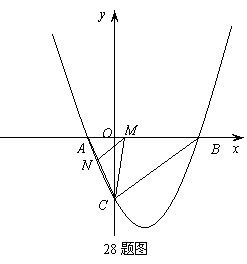
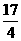 ,
,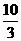 ,
,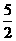 ,2,
,2,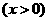 的图象如图.
的图象如图.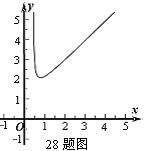
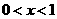 时,
时,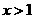 时,
时,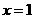 时函数
时函数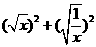
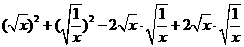
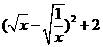
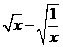 =0,即
=0,即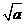 时,它的周长最小,最小值为
时,它的周长最小,最小值为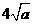 .
. 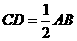 ,∴CD=BD.
,∴CD=BD.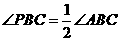 ,
,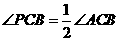 .
.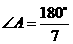 .∴该三角形三个内角的度数分别为
.∴该三角形三个内角的度数分别为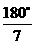 、
、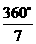 、
、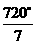 .
.
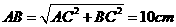 .∵P为BC的中点,∴PB=4cm.
.∵P为BC的中点,∴PB=4cm.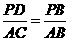 ,即
,即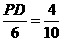 ,∴PD =2.4(cm) .
,∴PD =2.4(cm) .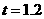 时,
时,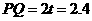 (cm)
(cm) 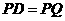 ,即圆心
,即圆心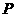 到直线
到直线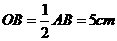 .
.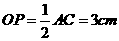 .
. 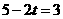 或
或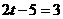 ,∴
,∴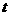 =1或4.
=1或4.