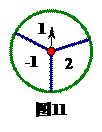
45. (2011河北,21,8分)如图11,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
(1)若小静转动转盘一次,求得到负数的概率;
(2)小宇和小静分别转动转盘一次,若两人得到的数相同,则称两人“不谋而合”.用列表法(或画树状图)求两人“不谋而合”的概率.
[答案](1)P(得到负数)=
(2)列表:
|
|
-1 |
1 |
2 |
|
-1 |
(-1,-1) |
(-1,1) |
(-1,2) |
|
1 |
(1,-1) |
(1,1) |
(1,2) |
|
2 |
(2,-1) |
(2,1) |
(2,2) |
P(两人“不谋而合”)=
41. (2011重庆市潼南,22,10分)端午节吃粽子是中华民族的传统习俗,一超市为了吸引消费者,增加销售量,
特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一
次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两
个转盘的指针所指字母都相同时,消费者就可以获得一次八折优惠价购买粽子的机会.
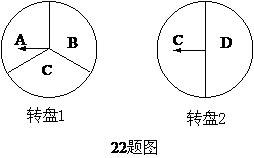
(1)用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;
(2)若一名消费者只能参加一次游戏,则他能获得八折优惠价购买粽子的概率是多少?
[答案]解: (1)解法一:
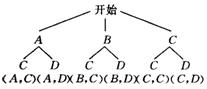
--------------4分
--------------6分
解法二:
 转盘2 转盘2转盘1 |
C |
D |
|
A |
(A,C) |
(A,D) |
|
B |
(B,C) |
(B,D) |
|
C |
(C,C) |
(C,D) |
(2)∵ 当两个转盘的指针所指字母都相同时的结果有一个,
∴P=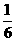 -----------------------------10分
-----------------------------10分
39. (2011江苏盐城,21,8分)小明有3支水笔,分别为红色、蓝色、黑色;有2块橡皮,分别为白色、灰色.小明从中任意取出1支水笔和1块橡皮配套使用.试用树状图或表格列出所有可能的结果,并求取出红色水笔和白色橡皮配套的概率.
[答案]解法一:画树状图:
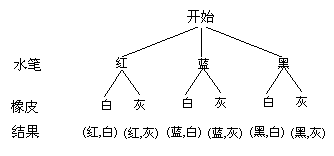

P(红色水笔和白色橡皮配套)= .
解法二:用列表法:
|
白 |
灰 |
||||||
|
红 |
(红,白) |
(红,灰) |
||||||
|
蓝 |
(蓝,白) |
(蓝,灰) |
||||||
|
黑 |
(黑,白) |
(黑,灰) |
P(红色水笔和白色橡皮配套)= .
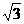 .(1分)∴正三角形的面积为
.(1分)∴正三角形的面积为 ×2×
×2×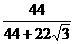 (7分)≈0.54.(8分)
(7分)≈0.54.(8分)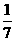 .
. ,所以
,所以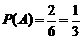 ,
,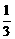 .
. ;
;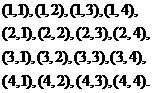
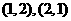 ,所以其概率为
,所以其概率为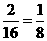 .
. ⑵A方案P(甲胜)=
⑵A方案P(甲胜)= ,B方案P(甲胜)=
,B方案P(甲胜)= 故选择A方案甲的胜率更高.
故选择A方案甲的胜率更高.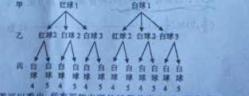
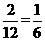 ;
;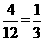 。
。