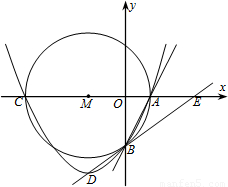
摘要:解:(1). ∵y轴和直线l都是⊙C的切线 ∴OA⊥AD BD⊥AD 又∵ OA⊥OB ∴∠AOB=∠OAD=∠ADB=90° ∴四边形OADB是矩形 ∵⊙C的半径为2 ∴AD=OB=4 ∵点P在直线l上 ∴点P的坐标为(4.p) 又∵点P也在直线AP上 ∴p=4k+3 (2)连接DN ∵AD是⊙C的直径 ∴ ∠AND=90° ∵ ∠AND=90°-∠DAN.∠ABD=90°-∠DAN ∴∠AND=∠ABD 又∵∠ADN=∠AMN ∴∠ABD=∠AMN ----4分 ∵∠MAN=∠BAP ----5分 ∴△AMN∽△ABP ----6分 (3)存在. ----7分 理由:把x=0代入y=kx+3得y=3.即OA=BD=3 AB= ∵ S△ABD= AB·DN=AD·DB ∴DN== ∴AN2=AD2-DN2= ∵△AMN∽△ABP ∴ 即 --8分 当点P在B点上方时. ∵AP2=AD2+PD2 = AD2+2 =42+2 =16(k2+1) 或AP2=AD2+PD2 = AD2+2 =42+2 =16(k2+1) S△ABP= PB·AD= ∴ 整理得k2-4k-2=0 解得k1 =2+ k2=2- ----9分 当点P在B 点下方时. ∵AP2=AD2+PD2 =42+2 =16(k2+1) S△ABP= PB·AD=[- ∴ 化简.得k2+1=- 解得k=-2 综合以上所得.当k=2±或k=-2时.△AMN的面积等于 -10分
网址:http://m.1010jiajiao.com/timu3_id_495309[举报]
 如图,直线y=2x-4与x轴交于点A,与y轴交于点B,以x轴上点M为圆心,过A、B两点作⊙M与x轴交于另一点C.
如图,直线y=2x-4与x轴交于点A,与y轴交于点B,以x轴上点M为圆心,过A、B两点作⊙M与x轴交于另一点C.(1)求⊙M的半径及圆心M的坐标;
(2)①求经过A、B、C三点的抛物线的顶点D的坐标;
②求证:DB是⊙M的切线;
(3)若半径为1的⊙P与x轴和直线BD都相切,请直接写出点P的坐标. 查看习题详情和答案>>
已知:抛物线y=ax2+(1-a)x+(5-2a)与x轴负半轴交于点A,与x轴正半轴交于点B,与y轴交于点C,tan∠CAO-tan∠CBO=2.
(1)当抛物线的解析式及顶点D的坐标;
(2)当线段OB与线段OC长度相等时,在抛物线的对称轴上取一点P,以点P为圆心作圆,使它与x轴和直线BD都相切,求点P的坐标. 查看习题详情和答案>>
(1)当抛物线的解析式及顶点D的坐标;
(2)当线段OB与线段OC长度相等时,在抛物线的对称轴上取一点P,以点P为圆心作圆,使它与x轴和直线BD都相切,求点P的坐标. 查看习题详情和答案>>
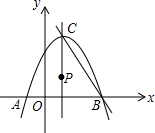 如图,已知抛物线
如图,已知抛物线 ,与
,与 轴交于A、B两点,点
轴交于A、B两点,点 为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为
为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为 ,当⊙P与
,当⊙P与