0 49516 49524 49530 49534 49540 49542 49546 49552 49554 49560 49566 49570 49572 49576 49582 49584 49590 49594 49596 49600 49602 49606 49608 49610 49611 49612 49614 49615 49616 49618 49620 49624 49626 49630 49632 49636 49642 49644 49650 49654 49656 49660 49666 49672 49674 49680 49684 49686 49692 49696 49702 49710 447348
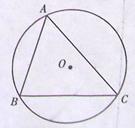
 ,点A为弦BC所对优弧上任意一点(B,C两点除外)。
,点A为弦BC所对优弧上任意一点(B,C两点除外)。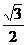 ,cos30°=
,cos30°= .)
.)
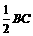 =
= .
.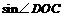 =
=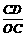 ,即
,即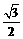 ,
,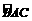 的中点时,△ABC面积的最大值.
的中点时,△ABC面积的最大值.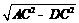 =
=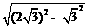 =3.
=3.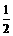 =3
=3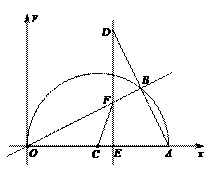
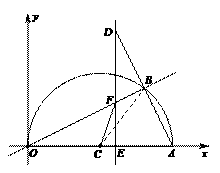

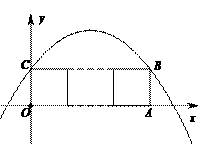 ∴∠ACB=2∠AOB=60°,
∴∠ACB=2∠AOB=60°,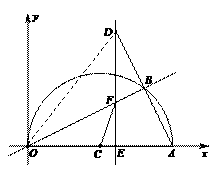
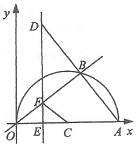
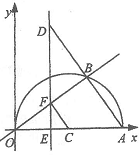


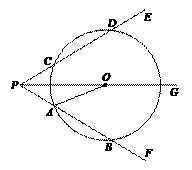

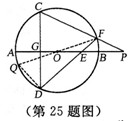 ∵FQ是⊙O直径,∴∠FDQ=90°.
∵FQ是⊙O直径,∴∠FDQ=90°.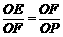 .∴OE·OP=OF2=r2.
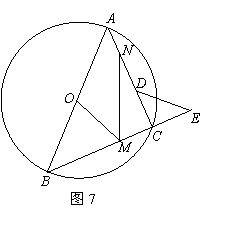
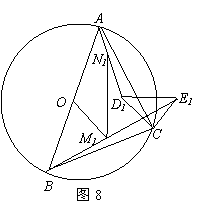
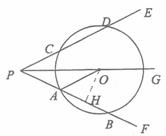
.∴OE·OP=OF2=r2.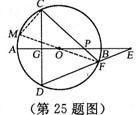 理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.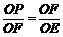 ,∴OE·OP=OF2=r2.
,∴OE·OP=OF2=r2. 为
为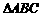 外接圆的直径,
外接圆的直径,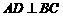 ,垂足为点
,垂足为点 ,
,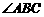 的平分线交
的平分线交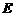 ,连接
,连接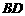 ,
, .
.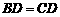 ;
; 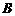 ,
,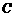 三点是否在以
三点是否在以 为圆心,以
为圆心,以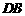 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.

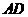 为直径,
为直径,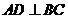 ,
,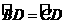 .∴
.∴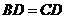 . ································································· 3分
. ································································· 3分 .
. ,
,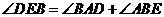 ,
, ,
,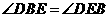 .∴
.∴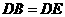 .··································································· 6分
.··································································· 6分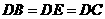 .
.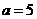 ,
,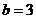 时,
时, 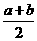 与
与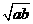 的大小关系是_________________.
的大小关系是_________________.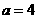 ,
, 时,
时, 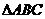 为圆O的内接三角形,
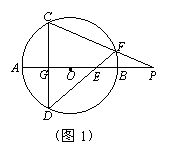
为圆O的内接三角形,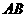 为直径,过C作
为直径,过C作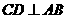 于D,设
于D,设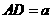 ,BD=b.
,BD=b.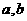 表示线段OC,CD;
表示线段OC,CD;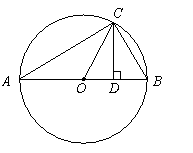

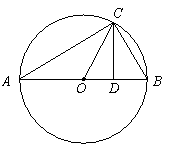 ●探究证明:
●探究证明: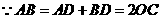 ,
,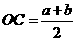 …………………3分
…………………3分 AB为⊙O直径,
AB为⊙O直径, .
.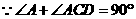 ,
,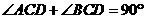 ,
, ∽△
∽△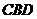 . …………………4分
. …………………4分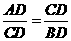 .
.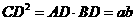 ,
,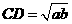 .
…………………5分
.
…………………5分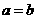 时,
时,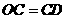 ,
,  时,
时, ,
, 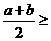
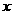 米,则另一边长为
米,则另一边长为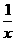 米,设镜框周长为l米,则
米,设镜框周长为l米,则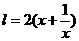 ≥
≥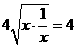 .
……………9分
.
……………9分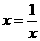 ,即
,即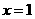 (米)时,镜框周长最小.
(米)时,镜框周长最小.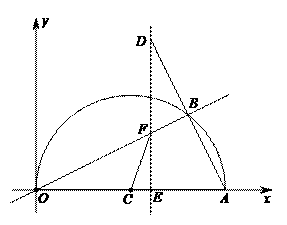
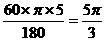 ; ……4分
; ……4分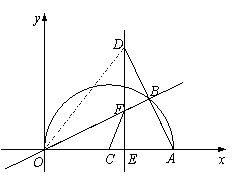


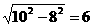 ,
,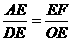 ,即
,即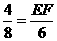 ,∴EF=3;……4分
,∴EF=3;……4分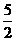 ,
,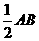 ,
,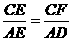 ,即
,即 ,解得:
,解得: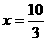 ,
,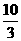 ,0);
,0);



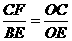 ,
,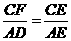 ,
,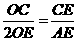 ,
,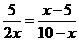 , 解得
, 解得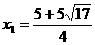 ,
, 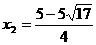 <0(舍去),
<0(舍去), ,0);
,0);

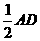 =AB,∠BEA=∠BAO
=AB,∠BEA=∠BAO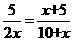 , 解得
, 解得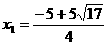 ,
, 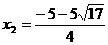 <0(舍去),
<0(舍去),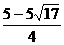 ,0),
,0),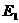 (
(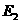 (
(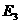 (
(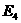 (
(


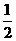 AB,……1分
AB,……1分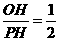 ,∴PH=2OH, ……1分
,∴PH=2OH, ……1分 , ∴
, ∴ , ……1分
, ……1分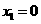 (不合题意,舍去),
(不合题意,舍去),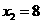 ,
,
