0 49809 49817 49823 49827 49833 49835 49839 49845 49847 49853 49859 49863 49865 49869 49875 49877 49883 49887 49889 49893 49895 49899 49901 49903 49904 49905 49907 49908 49909 49911 49913 49917 49919 49923 49925 49929 49935 49937 49943 49947 49949 49953 49959 49965 49967 49973 49977 49979 49985 49989 49995 50003 447348
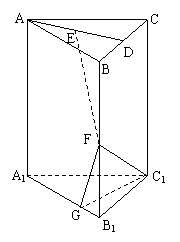 如图,已知直三棱柱ABC-A1B1C1中,AB=AC,D为
如图,已知直三棱柱ABC-A1B1C1中,AB=AC,D为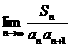 的值.
的值.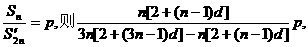
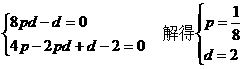 ,即等差数列的通项公式是an=2n-1.
,即等差数列的通项公式是an=2n-1.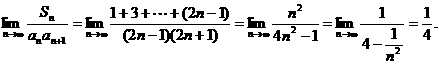
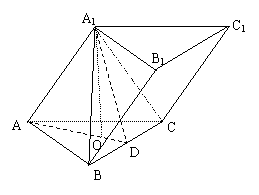 斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面的射影O是△ABC的中心,异面直线AB与CC1所成的角为45°.
斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面的射影O是△ABC的中心,异面直线AB与CC1所成的角为45°.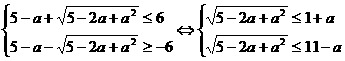
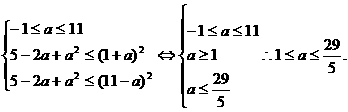
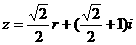 ,
,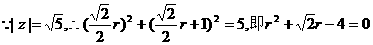
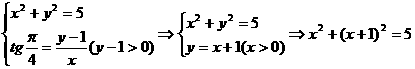
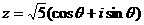 则
则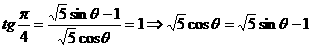
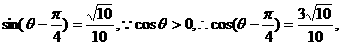
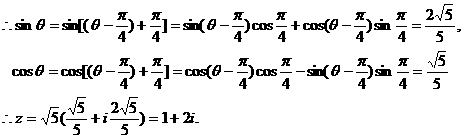
 (Ⅰ)求此正三棱锥的体积;
(Ⅰ)求此正三棱锥的体积;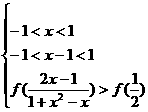
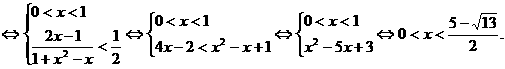
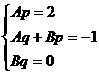 ,∵q≠0,∴B=0,∴=-2,
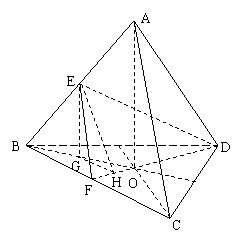
,∵q≠0,∴B=0,∴=-2,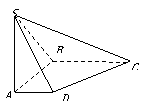 (2001w(18)12分)如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=
(2001w(18)12分)如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=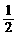 .
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.