18.(12分)某商店采用“购物摸球中奖”促销活动,摸奖处袋中装有10个号码为n(1≤n≤10,n∈N*),重量为f(n)=n2-9n+21(g)的球.摸奖方案见下表:
|
方 案 |
摸奖办法 |
奖 金 |
|
① |
凡一次购物在[50,100]元者,摸球1个,若球的重量小于该球的号码数,则中奖 |
10元 |
|
② |
凡一次购物在100元以上者,同时摸出两球,若两球的重量相等,则中奖 |
40元 |
说明:凭购物发票到摸奖处,按规定方案摸奖;这些球以等可能性从袋中摸出;假定符合条件的顾客均参加摸奖.
试比较方案①与②的中奖概率的大小.
解:当球的重量小于号码数时,有
n2-9n+21<n,解得3<n<7.
∵n∈N*,∴n的取值为4,5,6.
∴所求的概率为P1=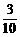 .
.
设第n号与第m号的两个球的重量相等,不妨设n<m,则有n2-9n+21=m2-9m+21,
即(n-m)(m+n-9)=0.
∵n≠m,∴m+n=9.
∴(n,m)的取值满足(1,8),(2,7),(3,6),(4,5).
∴所求的概率为P2=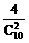 =
=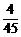 .
.
∴P1>P2,即方案①的中奖概率大.
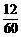 =
=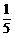 .
.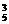 (
(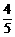 )2=0.0512.
)2=0.0512.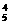 (
(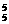 (
(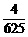 +
+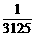 =0.00672.
=0.00672.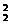 0.72·C
0.72·C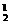 0.8×0.2=0.1568.
0.8×0.2=0.1568.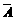 =“他第一次没有遇到红灯”,
=“他第一次没有遇到红灯”,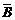 =“他第二次没有遇到红灯”.
=“他第二次没有遇到红灯”.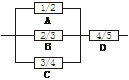
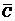 、
、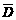 ,依题意各事件是相互独立的.
,依题意各事件是相互独立的.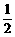 )×
)×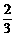 +
+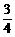 )=
)=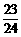 .
.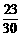 .
.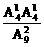 =
=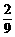 .
.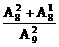 =
=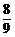 (或P2=1-
(或P2=1-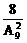 =
=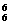 种排法,其中后排每人均比前排同学高,共有A
种排法,其中后排每人均比前排同学高,共有A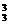 A
A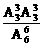 =
=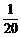 .
.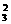 ·0.82·0.2+0.83=0.896.
·0.82·0.2+0.83=0.896.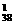 种,
种,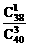 =
=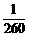 .
.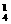 C
C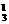 .
.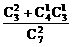 =
=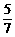 .
.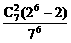 B.
B.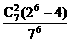
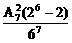 D.
D.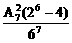
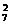 (26-2)(每人生日有两种可能,集中在同一天也为2种).所以P=
(26-2)(每人生日有两种可能,集中在同一天也为2种).所以P=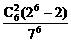 ,故选A.
,故选A.