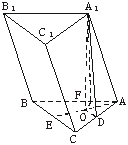
摘要:斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形.顶点A1在底面的射影O是△ABC的中心.异面直线AB与CC1所成的角为45°. (1)求证:AA1⊥平面A1BC, (2)求二面角A1-BC-A的平面角的正弦值, (3)求这个斜三棱柱的体积. (1)由已知可得A1-ABC为正三棱锥.∠A1AB=45° ∴∠AA1B=∠AA1C=90°即AA1⊥A1B,AA1⊥A1C ∴AA1⊥平面A1BC (2)连AO并延长交BC于D,则AD⊥BC.连A1D, 则∠ADA1为所求的角.由已知可得 AD=Absin60°=, AA1=Absin45°=,∴sin∠ADA1= (3)在Rt△AA1D中.A1D=∴A1O= ∴V柱=S△ABC·A1O=·4·sin60°·. *选做题:已知函数f(x)=loga 的定义域, 是增函数.求a的取值范围. 解:(1)由ax->0 得x>.即f (2)设x1>x2>,则a ∴(ax1-)-(ax2-)=(>0, ∴ax1-> ax2-∵f(x)是增函数.∴f(x1)>f(x2)∴a>1. 高考数学中档题精选(3)
网址:http://m.1010jiajiao.com/timu3_id_499067[举报]
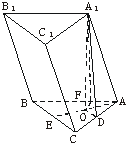
斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面ABC的射影O是D![]() ABC的中心,AA1与AB的夹角是45°.
ABC的中心,AA1与AB的夹角是45°.
(1)求证AA1^平面A1BC;
(2)求此棱柱的侧面积.
查看习题详情和答案>>