0 49820 49828 49834 49838 49844 49846 49850 49856 49858 49864 49870 49874 49876 49880 49886 49888 49894 49898 49900 49904 49906 49910 49912 49914 49915 49916 49918 49919 49920 49922 49924 49928 49930 49934 49936 49940 49946 49948 49954 49958 49960 49964 49970 49976 49978 49984 49988 49990 49996 50000 50006 50014 447348
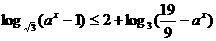 ,(a>0且a≠1).
,(a>0且a≠1).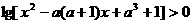 ,(a>0且a≠1).
,(a>0且a≠1).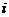 ,z2=65
,z2=65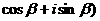
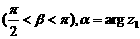 且
且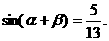
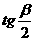 ;
; 点,F在PC上且PF=
点,F在PC上且PF=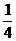 PC.
PC.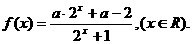
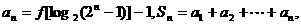 求
求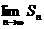 ;
;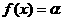 在(-∞,0)上有解,试证
在(-∞,0)上有解,试证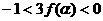 .
.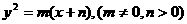 的焦点为原点,C的准线与直线
的焦点为原点,C的准线与直线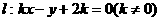 的交点M在x轴上,
的交点M在x轴上,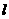 与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).
与C交于不同的两点A、B,线段AB的垂直平分线交x轴于点N(p,0).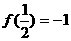 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有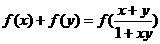 .
.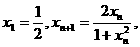 求
求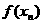 ;
;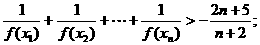
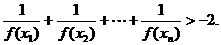

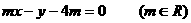 与点P所在
与点P所在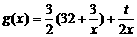 时,则当年的产销量相等.
时,则当年的产销量相等.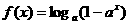 (其中a>0,且a≠1),解关于x的不等式
(其中a>0,且a≠1),解关于x的不等式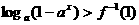
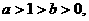 不等式
不等式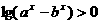 的解集为M
的解集为M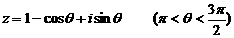 且
且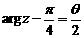 .
.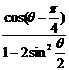 的值.
的值. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为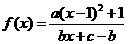 (a、b、
(a、b、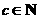 )的图象按
)的图象按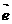 =(-1,0)平移后得到的图象关于原点对称,f(2)=2,f(3)<3.
=(-1,0)平移后得到的图象关于原点对称,f(2)=2,f(3)<3.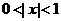 ,
,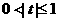 求证:
求证: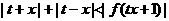 ;
;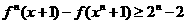 .
.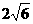 ,且
,且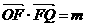 ,
,
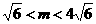 时,求向量
时,求向量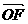 与
与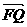 的夹角
的夹角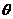 的取值范围;
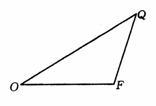
的取值范围;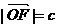 ,
,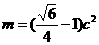 时,若以O为中心,F为焦点的双曲线经过点Q,当
时,若以O为中心,F为焦点的双曲线经过点Q,当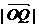 取得最小值时,求此双曲线的方程.
取得最小值时,求此双曲线的方程.