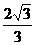22.(14分)解:(1)抛物线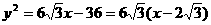 的项点为
的项点为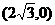 (文2理1分)
(文2理1分)
准线为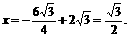 ……………………………(文4,理2分)
……………………………(文4,理2分)
设双曲线G为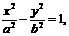 则有
则有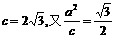 ,可得,a2=3,b2=9.
,可得,a2=3,b2=9.
∴双曲线G的方程为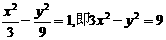 .……………………(文6,理4分)
.……………………(文6,理4分)
(2)①由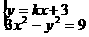 ,得
,得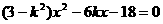 ………………………………(文7分)
………………………………(文7分)
又由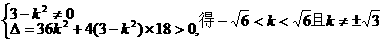 .………(文8,理5分)
.………(文8,理5分)
设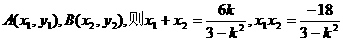 …………………………(文9分)
…………………………(文9分)
∵若原点O在AB为直径的圆上,有OA⊥OB,KOA·KOB=-1,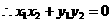 ,即
,即
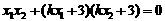 ……(文10,理6分) 化简为
……(文10,理6分) 化简为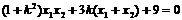
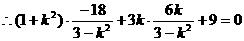 ………(文12,理7分)解得,
………(文12,理7分)解得,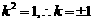 .
.
 故,当k=±1时,原点O在AB为直径的圆上.………(文14,理8分)
故,当k=±1时,原点O在AB为直径的圆上.………(文14,理8分)
②设这样的实数k存在,则有
|
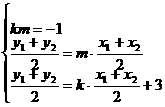
由②③得,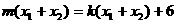 …………………………………………(12分)
…………………………………………(12分)
即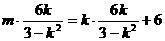 ,推得km=3,……………………………………(13分)
,推得km=3,……………………………………(13分)
这与km=-1矛盾,所以适合条件的k不存在.………………………(14分)
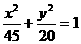 在第三象限内一点,且它与两焦点连线互相垂直。若点P到
在第三象限内一点,且它与两焦点连线互相垂直。若点P到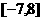 (B)
(B)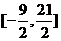 (C)
(C)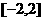 (D)
(D)
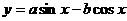 的一条对称轴方程是
的一条对称轴方程是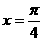 ,则直线
,则直线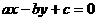 的倾斜角为 ( )
的倾斜角为 ( ) (B)
(B)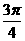 (C)
(C)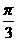 (D)
(D)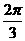
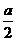 ,则三棱锥P-BDQ的体积为 ( )
,则三棱锥P-BDQ的体积为 ( )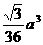 (B)
(B)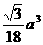 (C)
(C)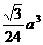 (D)不确定
(D)不确定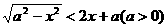 的解集是 ( )
的解集是 ( )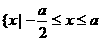 } (B)
} (B)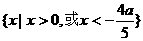
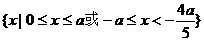 (D)
(D)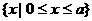
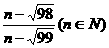 ,则数列{an}的前30项中最大项是 ( )
,则数列{an}的前30项中最大项是 ( )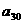 (B)
(B)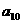 (C)
(C)
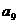 (D)
(D)
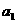
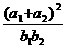 的取值范围是 (
)
的取值范围是 (
)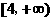 (B)
(B)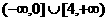 (C)
(C)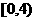 (D)
(D)
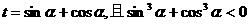 ,则t的取值范围是 ( )
,则t的取值范围是 ( )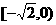 (B)
(B)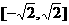
 (D)
(D)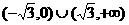
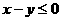 (B)
(B)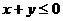 (C)
(C)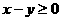 (D)
(D)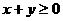
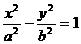 ,(a>0,b>0)的一条准线与两条渐近线交于A,B两点,相应焦点为
,(a>0,b>0)的一条准线与两条渐近线交于A,B两点,相应焦点为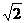 (B)
(B) (C)2
(C)2  (D)
(D)