摘要： 已知f(x)=sin2x-2(a-1)sinxcosx+5cos2x+2-a,若对于任意的实数x恒有|f(x)|≤6成立.求a的取值范围. 解:fsin2x+2cos2x+5-a=sin+5-a.(ψ为一定角.大小与a有关). ∵x∈R,∴[f(x)]max=5-a+,[f(x)]min=5-a-. 由|f(x)|≤6,得
网址：http://m.1010jiajiao.com/timu3_id_499066[举报]
已知向量
=(
sin2x+2，cosx)，
=(1，2cosx)，设函数f(x)= ·．
(I)求f(x)的最小正周期与单调递增区间；
(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，若A=，b=f(
),ΔABC的面积为
，求a的值
查看习题详情和答案>>
已知向量
=(
sin2x+2，cosx)，
=(1，2cosx)，设函数f(x)= ·．
(I)求f(x)的最小正周期与单调递增区间；
(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，若a=，f(A)=4，求b+c的最大值．
查看习题详情和答案>>
已知向量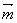
=(
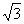sin2x+2，cosx)，
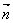=(1，2cosx)，设函数f(x)= ·．
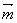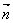(I)求f(x)的最小正周期与单调递增区间；
(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，若a=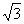，f(A)=4，求b+c的最大值．
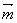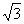=(sin2x+2，cosx)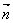，=(1，2cosx)，设函数f(x)= 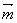·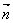．(I)求f(x)的最小正周期与单调递增区间；
(Ⅱ)在△ABC中，a，b，c分别是角A，B，C的对边，若a=
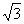，f(A)=4，求b+c的最大值．
=(
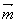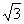sin2x+2，cosx)，
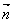=(1，2cosx)，设函数f(x)= 
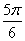),ΔABC的面积为
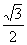，求a的值