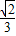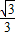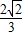摘要： 已知正三棱锥A-BCD的边长为a.E.F分别为AB.BC的中点.且AC⊥DE. (Ⅰ)求此正三棱锥的体积, (Ⅱ)求二面角E-FD-B的正弦值. 解:(Ⅰ)作AO⊥平面BCD于O,由正三棱锥的性质 可知O为底面中心.连CO,则CO⊥BD,由三垂线定理 知AC⊥BD.又AC⊥ED,∴AC⊥平面ABD,∴AC⊥AD, AB⊥AC,AB⊥AD.在Rt△ACD中.由AC2+AD2=2AC2=a2 可得:AC=AD=AB=. ∴V=VB-ACD=. (Ⅱ)过E作EG⊥平面BCD于G.过G作GH⊥FD于H.连EH.由三垂线定理知EH⊥FD,即∠EHG为二面角E-FD-B的平面角. ∵EG＝AO 而AO＝,∴EG=. 又∵ED＝∵EF∥AC.∴EF⊥DE.∴在Rt△FED中.EH＝∴在Rt△EGH中.sin∠EHG＝ *选做题:定义在区间满足:①对任意x.y∈=f时.f(x)>0. 为奇函数, +f. 解:+f=0. 又令x∈.而f= ∴f在上是奇函数. (Ⅱ)令-1<x1<x2<1,则x1-x2<0,1-x1x2>0, 于是f(x1)-f(x2)=f(x1)+f(-x2)=f()>0,即f(x1)>f(x2),所以f(x)在定义域上为减函数.从而f等价与不等式 高考数学中档题精选(2)

网址：http://m.1010jiajiao.com/timu3_id_499064[举报]