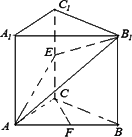
摘要:如图.已知直三棱柱ABC-A1B1C1中.AB=AC.D为 BC中点.F为BB1上一点.BF=BC=2,FB1=1. (1) 求证:AD⊥平面BB1C1C; (2) 若E为AD上不同于A.D的任一点.求证:EF⊥FC1; (3) 若A1B1=3,求FC1与平面AA1B1B所成角的大小. 解:如图.(1)∵AB=AC且D为BC中点.∴AD⊥BC ∵ABC-A1B1C1是直三棱柱.∴平面ABC⊥平面BB1C1C ∴AD⊥平面BB1C1C. (2)连结DF,DC1,由已知可求得DF=,FC1=DC1=, DF2+FC12=DC12,∴∠DFC1=90°.即DF⊥CF1.由三垂线 定理知EF⊥FC1. (3)作C1G⊥A1B1, 垂足为G,则C1G⊥平面AA1B1B,∴∠C1FG即为所求的角. 在Rt△ABD中.可求得AD=2.由C1G·A1B1=AD·BC 得 C1G = ∴sin∠C1FG= ∴∠C1FG=arcsin. *选做题:设函数f(x)的定义域为R.对于任意实数x.y.总有f.且当x>0时.0<f(x)<1. =1.且x<0时.f(x)>1, 在R上单调递减, |f(x2)f(y2)>f|f=1,a∈R}.若M∩N=φ.试确定a的取值范围. 证明:中.令x=1,y=0,得f.因为0<f=1. 取y=-x>0,则f=1,即f<1,∴f(x)>1. (2)设x1<x2.则x2-x1>0.于是.0<f(x2-x1)<1,f(x1)>0, ∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0, ∴f(x)在R上单调递减. (3)解:由f(x2)f(y2)>f(1).得f(x2+y2)>f(1).即x2+y2<1, 由f.得ax-y+2=0 由若M∩N=φ.得.解得-≤a≤.
网址:http://m.1010jiajiao.com/timu3_id_499070[举报]
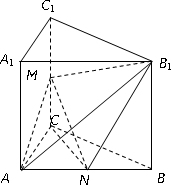
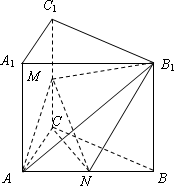
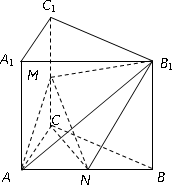
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4.
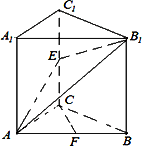
(1)当E是棱CC1的中点时,求证:CF∥平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A-EB1-B的大小是45°?若存在,求出CE的长,若不存在,请说明理由.