37. (2011广东茂名,19,7分)从甲学校到乙学校有 、
、 、
、 三条线路,从乙学校到丙学校有
三条线路,从乙学校到丙学校有 、
、 二条线路.
二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;(4分)
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了 线路的概率是多少? (3分)
线路的概率是多少? (3分)
[答案]解:(1)利用列表或树状图的方法表示从甲校到丙校的线路所有可能出现的结果如下:
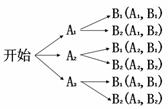
|
|
A1 |
A2 |
A3 |
|
B1 |
(A1 、B1) |
(A2 、B1) |
(A3、B1) |
|
B2 |
(A1 、 B2) |
(A2、 B2) |
(A3 、B2 ) |
(2) 小张从甲学校到丙学校共有6条不同的线路,其中经过B1线路有3条,
所以:P(小张恰好经过了 线路的概率)=
线路的概率)= .·
.·
36. (2011贵州贵阳,19,10分)
一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3、4、5、
x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表:
|
摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
|
“和为8”出现的频数 |
2 |
10 |
13 |
24 |
30 |
37 |
58 |
82 |
110 |
150 |
|
“和为8”出现的频率 |
0.20 |
0.50 |
0.43 |
0.40 |
0.33 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是______;(4分)
(2)如果摸出的这两个小球上数字之和为9的概率是,那么x的值可以取7吗?请用列表法或画树状图法说明理由;如果x的值不可以取7,请写出一个符合要求的x值.(6分)
[答案]解:(1)0.33.
(2)x不可以取7,画树状图法说明如下:

从图中可知,数字和为9的概率为=.
当x=6时,摸出的两个小球上数字之和为9.
32. (2011湖北武汉市,20,7分)(本题满分7分)经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
[答案]解法1:
(1)根据题意,可以画出如下的“树形图”: 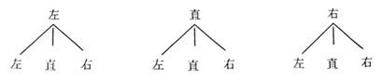
∴这两辆汽车行驶方向共有9种可能的结果
(2)由(1)中“树形图”知,至少有一辆汽车向左转的结果有5种,且所有结果的可能性相等
∴P(至少有一辆汽车向左转)=5/9
解法2:根据题意,可以列出如下的表格:
|
|
左 |
直 |
右 |
|
左 |
(左,左) |
(左,直) |
(左,右) |
|
直 |
(直,左) |
(直,直) |
(直,右) |
|
右 |
(右,左) |
(右,直) |
(右,右) |
以下同解法1(略)
31. (2011江苏无锡,22,7分)(本题满分7分)一不透明的袋子中装有4个球,它们除了上面分别标有的号码1、2、3、4不同外,其余均相同。将小球搅匀,并从袋中任意取出一球后放回;再将小球搅匀,并从袋中再任意取出一球。求第二次取出球的号码比第一次的大的概率。(请用“画树状图”或“列表”的方法给出分析过程,并写出结果)
 [答案].解:(1)树状图: 第一次
第二次
列表:
[答案].解:(1)树状图: 第一次
第二次
列表:
|
树状图或列表正确 …………………………(4分)
∴第一次与第二次的号码组合共有16种不同的情况,其中第二次取出球的号码比第一次的大的情况有6种,故第二次球的号码比第一次的大的概率是 = .…………………………………………………(7分)
30. (2011四川凉山州,22,8分)6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。
⑴从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少?
⑵从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少?


[答案]
解:⑴
⑵根据题意得:
|
|
A |
B |
C |
D |
E |
F |
 A A |
|
AB |
AC |
AD |
AE |
AF |
|
B |
BA |
|
BC |
BD |
BE |
BF |
|
C |
CA |
CB |
|
CD |
CE |
CF |
|
D |
DA |
DB |
DC |
|
DE |
DE |
|
F |
EA |
EB |
EC |
ED |
|
EF |
|
|
FA |
FB |
FC |
FD |
FE |
|
由上表可知,共有30种可能的结果,且每种结果的可能性相同,其中能进行平面镶嵌的结果有8种,分别是:AB, AD, BE, CF, BA, DA, EB, FC 。

29. (2011四川乐山22,10分)在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同。小明先从口袋里随机不放回地取出一个小球,记下数字为x;小红在剩下有三个小球中随机取出一个小球,记下数字y。
(1)计算由x、y确定的点(x,y)在函数 图象上的概率;
图象上的概率;
(2)小明、小红约定做一个游戏,其规则是:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜.这个游戏规则公平吗?说明理由;若不公平,怎样修改游戏规则才对双方公平?
[答案]
解:⑴.列表如下
|
X+Y |
1 |
2 |
3 |
4 |
|
1 |
- |
3 |
4 |
5 |
|
2 |
3 |
- |
5 |
6 |
|
3 |
4 |
5 |
- |
7 |
|
4 |
5 |
6 |
7 |
- |
∴
⑵列表如下
|
X·Y |
1 |
2 |
3 |
4 |
|
1 |
- |
2 |
3 |
4 |
|
2 |
2 |
- |
6 |
8 |
|
3 |
3 |
6 |
- |
12 |
|
4 |
4 |
8 |
12 |
- |
∵ ,
,
∴
∴这个游戏规则不公平
规则改为:“若x、y满足 ,则小明胜;若x、y满足
,则小明胜;若x、y满足 ,则小红胜”
,则小红胜”
∵ ,
,
∴




 ,P(妹妹胜)=
,P(妹妹胜)=
 ⑵A方案P(甲胜)=
⑵A方案P(甲胜)= ,B方案P(甲胜)=
,B方案P(甲胜)= 故选择A方案甲的胜率更高.
故选择A方案甲的胜率更高.

