0 49361 49369 49375 49379 49385 49387 49391 49397 49399 49405 49411 49415 49417 49421 49427 49429 49435 49439 49441 49445 49447 49451 49453 49455 49456 49457 49459 49460 49461 49463 49465 49469 49471 49475 49477 49481 49487 49489 49495 49499 49501 49505 49511 49517 49519 49525 49529 49531 49537 49541 49547 49555 447348
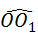 和
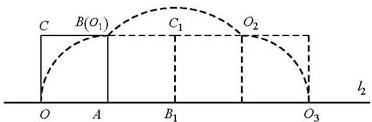
和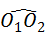 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.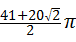 ?
?
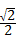 )π+
)π+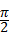 ,即可得出旋转次数.
,即可得出旋转次数.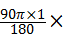 2+
2+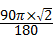 =(1+
=(1+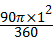 ×2+
×2+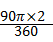 +2×
+2×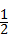 ×1=1+π.
×1=1+π.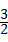 +
+

 时,∠PAD=60°;当PA的长度等于 2
时,∠PAD=60°;当PA的长度等于 2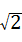 或
或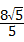 时,△PAD是等腰三角形;
时,△PAD是等腰三角形; 若△PAD是等腰三角形,则只能是PA=PD,
若△PAD是等腰三角形,则只能是PA=PD,
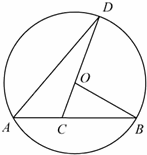
 过点O作OE⊥AB于E,
过点O作OE⊥AB于E,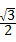 =
=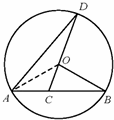 连接OA,
连接OA,
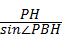 =20
=20
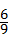 =
=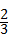 ;
;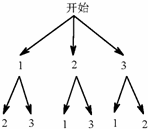
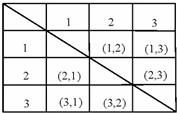
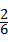 =
=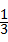 .
.
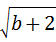 =0,求方裎
=0,求方裎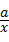 +bx=1的解.
+bx=1的解.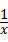 ﹣2x=1,得2x2+x﹣1=0,
﹣2x=1,得2x2+x﹣1=0,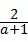 )÷(a2+1),其中a=
)÷(a2+1),其中a=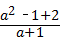 )•
)•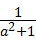 ,
,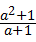 •
•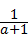 ,
,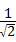 =
=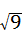 .
.