0 49451 49459 49465 49469 49475 49477 49481 49487 49489 49495 49501 49505 49507 49511 49517 49519 49525 49529 49531 49535 49537 49541 49543 49545 49546 49547 49549 49550 49551 49553 49555 49559 49561 49565 49567 49571 49577 49579 49585 49589 49591 49595 49601 49607 49609 49615 49619 49621 49627 49631 49637 49645 447348
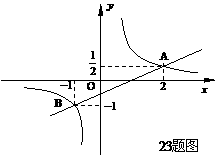
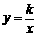 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数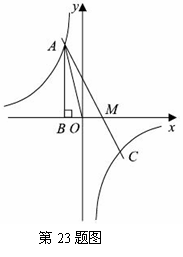

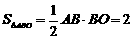
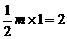 ,解得
,解得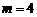 ,∴A (-1,4),
,∴A (-1,4),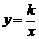 的图像上,∴4 =
的图像上,∴4 =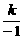 ,解得
,解得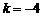 ,
,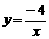 ,又∵反比例函数
,又∵反比例函数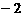 )
)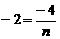 ,解得
,解得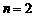 ,∴C (2,-2),
,∴C (2,-2),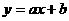 过点A (-1,4),C (2,-2)
过点A (-1,4),C (2,-2)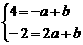 解方程组得
解方程组得 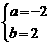
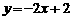 ;
;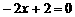 解得
解得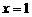 ,即点M(1,0)
,即点M(1,0)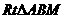 中,∵AB = 4,BM = BO +OM = 1+1 = 2,
中,∵AB = 4,BM = BO +OM = 1+1 = 2,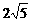 .
.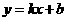 (k≠0)的图象与反比例函数
(k≠0)的图象与反比例函数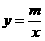 (m≠0)的图象相交于A、B两点.
(m≠0)的图象相交于A、B两点.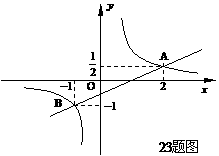
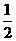 )
) ∴反比例函数的解析式为:
∴反比例函数的解析式为: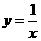 ---------------------4分
---------------------4分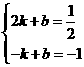
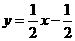 ----------------------6分
----------------------6分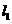 过点A(1,0)且与y轴平行,直线
过点A(1,0)且与y轴平行,直线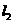 过点B(0,2)且与x轴平行,直线
过点B(0,2)且与x轴平行,直线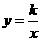 (k>0)的图象过点E且与直线
(k>0)的图象过点E且与直线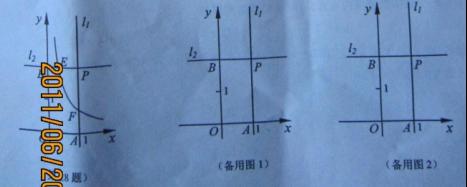
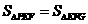
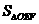 =2
=2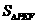
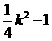 =
=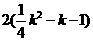

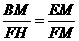 .
.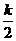 ,FM=PF=2-k
,FM=PF=2-k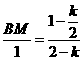 ,BM=
,BM=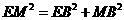 ,
,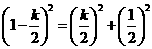 ,解得k=
,解得k=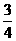 ,此时E点的坐标为(
,此时E点的坐标为(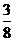 ,2)
,2)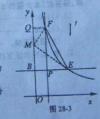
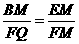
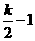 ,
,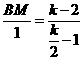 ,BM=2,
,BM=2,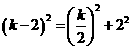
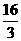 或0,但k=0不符合题意,所以k=
或0,但k=0不符合题意,所以k=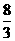 ,2),符合条件的E点坐标为
,2),符合条件的E点坐标为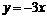 与双曲线
与双曲线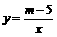 交于点P(-1,n).
交于点P(-1,n).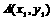 ,
,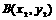 在双曲线
在双曲线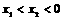 ,试比较
,试比较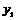 ,
,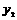 的大小.
的大小.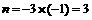 .····· 1分
.····· 1分 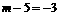 ,即m=2. ·· 3分
,即m=2. ·· 3分 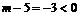 ,∴当x<0时,y随x的增大而增大
,∴当x<0时,y随x的增大而增大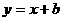 的图象经过点B(
的图象经过点B(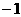 ,0),且与反比例函数
,0),且与反比例函数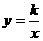 (
(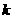 为不等于0的常数)的图象在第一象限交于点
为不等于0的常数)的图象在第一象限交于点 (1,
(1,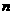 ).求:
).求: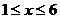 时,反比例函数
时,反比例函数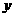 的取值范围.
的取值范围.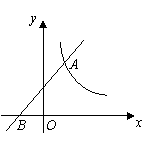

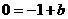 ∴b=1.
∴b=1. 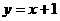
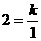 ,解得:
,解得: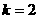
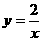
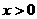 时,
时,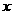 的增大而减少,
的增大而减少,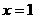 时,
时,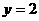 ;当
;当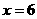 时,
时,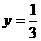
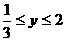
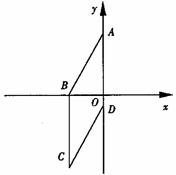
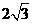 ),B(2,0)直线AB与反比例函数
),B(2,0)直线AB与反比例函数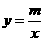 的图像交与点C和点D(-1,a).
的图像交与点C和点D(-1,a). α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.
α角(α为锐角),得到△OB′C′,当α为多少度时OC′⊥AB,并求此时线段AB′的长.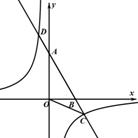
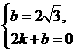 ,解得
,解得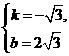 .∴直线AB的解析式为
.∴直线AB的解析式为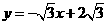 ;将D(-1,a)代入
;将D(-1,a)代入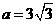 ,∴点D坐标为(-1,
,∴点D坐标为(-1,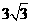 ),将D(-1,
),将D(-1,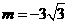 ,∴反比例函数的解析式为
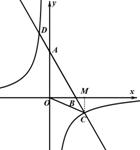
,∴反比例函数的解析式为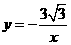 .
.
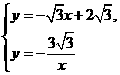 得
得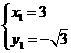 ,
,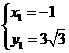 ,∴点C坐标为(3,
,∴点C坐标为(3,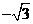 ),
),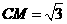 ,
,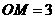 ,∴
,∴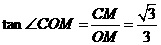 ,∴
,∴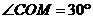 ,
,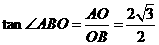 =
=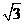 ,∴
,∴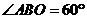 ,
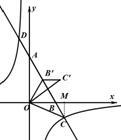
, .
.
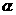 = ∠COC′=90°-30°=60°,∠BOB′=
= ∠COC′=90°-30°=60°,∠BOB′=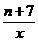 的图像的一支。
的图像的一支。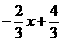 的图像与反比例函数图像交于点A,与x交于B,△AOB的面积为2,求n的值。
的图像与反比例函数图像交于点A,与x交于B,△AOB的面积为2,求n的值。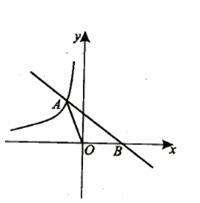
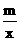 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.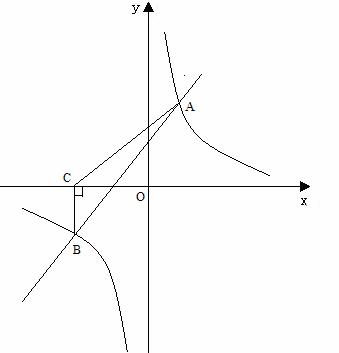
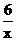 ,
,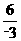 =-2,……………………………………………………………………(2分)
=-2,……………………………………………………………………(2分)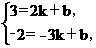
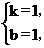
 (x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y=
(x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y=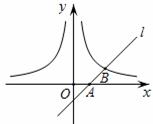
 ,得m=2.
,得m=2.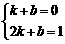 ,解得
,解得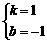
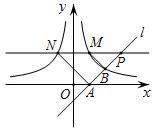
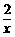 和y=
和y=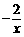 ,得M(1,2),N(-1,2)
,得M(1,2),N(-1,2)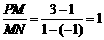 ,即M是PN的中点,
,即M是PN的中点,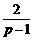 和N的横坐标x=-
和N的横坐标x=-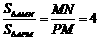 ,得MN=4PM
,得MN=4PM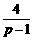 =4(p-
=4(p-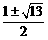
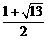
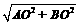 =
=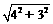 =5.
=5.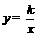 .
.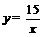 .
.