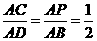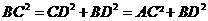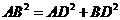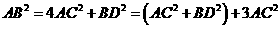0 49517 49525 49531 49535 49541 49543 49547 49553 49555 49561 49567 49571 49573 49577 49583 49585 49591 49595 49597 49601 49603 49607 49609 49611 49612 49613 49615 49616 49617 49619 49621 49625 49627 49631 49633 49637 49643 49645 49651 49655 49657 49661 49667 49673 49675 49681 49685 49687 49693 49697 49703 49711 447348
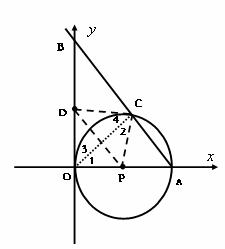
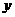 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与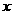 轴相交于点A(5,0),过点A的直线AB与
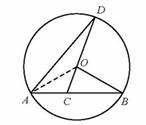
轴相交于点A(5,0),过点A的直线AB与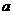 , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为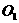 ,函数
,函数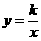 的图象经过点
的图象经过点 的值(用含
的值(用含


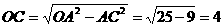
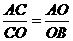 ,即
,即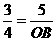 ,
,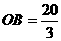 , ∴
, ∴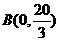
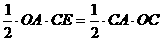 ,
,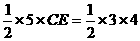 ,∴
,∴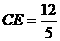 ,
,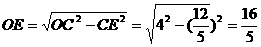 ∴
∴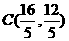 ,
,
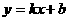 .
.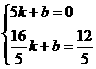 , 解得:
, 解得: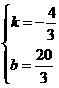 ,
,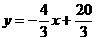 , ∴点
, ∴点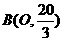 .
.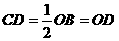 ,
,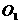 是DP的中点,圆心
是DP的中点,圆心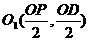 ,
,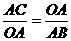 ,求得:AB=
,求得:AB=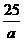 ,在Rt△ABO中,
,在Rt△ABO中,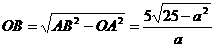 ,OD=
,OD=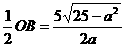 ,
,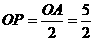
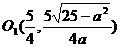 ,点
,点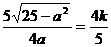 ,
∴
,
∴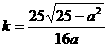
 .
.

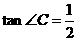 ,求弦MN的长.
,求弦MN的长.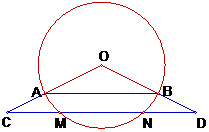
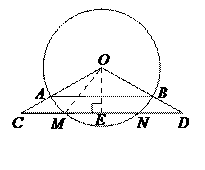

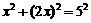 ,解得x1=
,解得x1=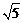 ,x2=
,x2=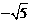 (舍去).∴OE=
(舍去).∴OE=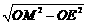 =
=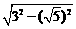 =2。∴MN=2ME=4.
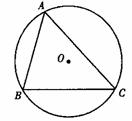
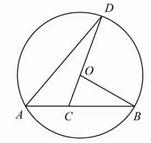
=2。∴MN=2ME=4. ,点A为弦BC所对优弧上任意一点(B,C两点除外)。
,点A为弦BC所对优弧上任意一点(B,C两点除外)。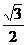 ,cos30°=
,cos30°= .)
.)
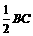 =
= .
.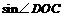 =
=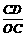 ,即
,即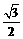 ,
,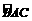 的中点时,△ABC面积的最大值.
的中点时,△ABC面积的最大值.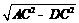 =
=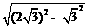 =3.
=3.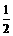 =3
=3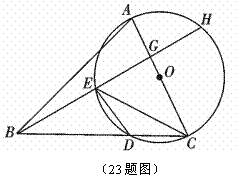


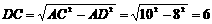 .
.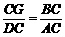
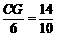 ∴
∴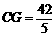
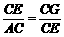 ∴
∴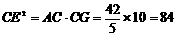
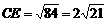 .
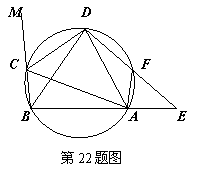
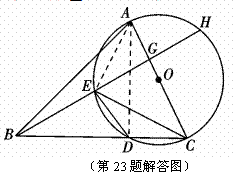
.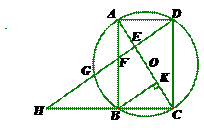 (1)求证:AE=CK;
(1)求证:AE=CK;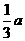 (
(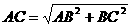 =
=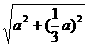 =
=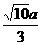 ,
,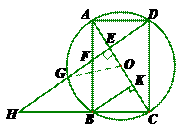 ∵S△ABC=
∵S△ABC=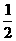 AB×BC=
AB×BC=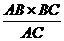 =
=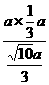 =
=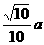 .
. ,则OE=
,则OE=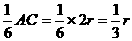 ,EG=6,
,EG=6,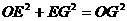 ,∴
,∴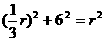 ,∴
,∴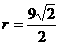 .
.
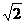 或
或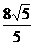 .
.
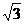 .
.
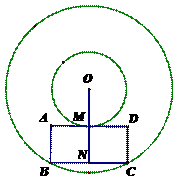
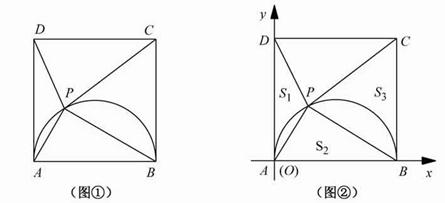
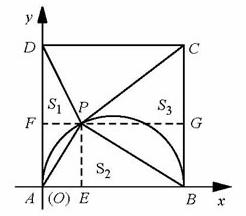
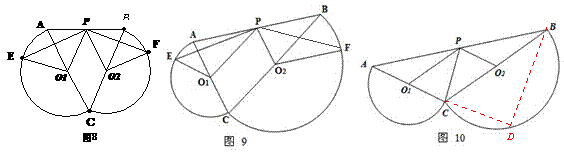
 、
、 P是AB的中点.
P是AB的中点. 上分别取点E、F,使
上分别取点E、F,使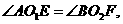 则有结论①
则有结论① 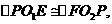 ②四边形
②四边形 是菱形.请给出结论②的证明;
是菱形.请给出结论②的证明;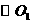 的切线,求证:
的切线,求证: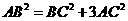

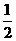 AC
AC