23、2011年长江中下游地区发生了特大早情.为抗旱保丰收,某地政府制定了农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备投资的金额与政府补的额度存在下表所示的函数对应关系.
|
型 号 金 额 投资金额x(万元) |
Ⅰ型设备 |
Ⅱ型设备 |
|||
|
X |
5 |
X |
2 |
4 |
|
|
补贴金额y(万元) |
y1=kx (k≠0) |
2 |
y2=ax2+bx (a≠0) |
2.4 |
3.2 |
(1)分别求y1和y2的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
考点:二次函数的应用.
分析:(1)根据图表得出函数上点的坐标,利用待定系数法求出函数解析式即可;
(2)根据y=y1+y2得出关于x的二次函数,求出二次函数最值即可.
解答:解:(1)y1=kx,将(5,2)代入得:
2=5k,
k=0.4,
y1=0.4x,
y2=ax2+bx,将(2,2.4),(4,3.2)代入得:
{2.4=4a+2b3.2=16a+4b,
解得:a=-0.2,b=1.6,
∴y2=-0.2x2+1.6x;
(2)假设投资购买Ⅰ型用x万元、Ⅱ型为(10-x)万元,
y=y1+y2=0.4x-0.2(10-x)2+1.6(10-x);
=-0.2x 2+2.8x-4,
当x=- b2a=7时,y= 4ac-b24a=5.8万元,
∴当购买Ⅰ型用7万元、Ⅱ型为3万元时能获得的最大补贴金额.
点评:此题主要考查了待定系数法求一次函数和二次函数解析式以及二次函数的最值问题,利用函数解决实际问题是考试的中热点问题,同学们应重点掌握.
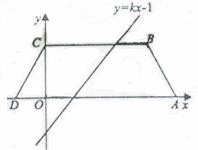 如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,求m的值.
如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,求m的值.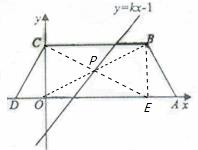 解:过B作BE⊥AD于E,连接OB、CE交于点P,
解:过B作BE⊥AD于E,连接OB、CE交于点P,
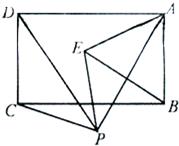 如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB,问△ABE是什么特殊三角形?请说明理由.
如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB,问△ABE是什么特殊三角形?请说明理由. 解不等式组.并把解集在数轴上表示出来.
解不等式组.并把解集在数轴上表示出来.
 解:延长BC,交x轴于点D,
解:延长BC,交x轴于点D,
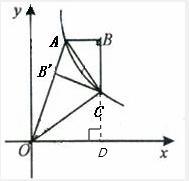
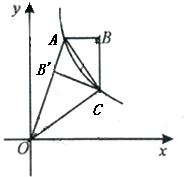 如图,双曲线 y=2x (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得AB′C,B′点落在OA上,则四边形OABC的面积是
如图,双曲线 y=2x (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得AB′C,B′点落在OA上,则四边形OABC的面积是 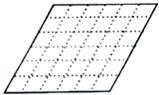 请将含60°顶角的菱形分割成至少含一个等腰梯形且面积相等的六部分,用实线画出分割后的图形.
请将含60°顶角的菱形分割成至少含一个等腰梯形且面积相等的六部分,用实线画出分割后的图形. 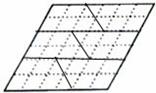 答案不唯一
答案不唯一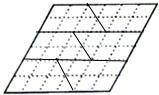 本题答案不唯一.
本题答案不唯一.