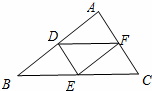
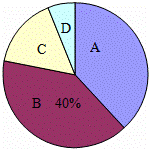
18、(2011•德州)2011年5月9日至14日,德州市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
|
等级 |
成绩(分) |
频数(人数) |
频率 |
|
A |
90-100 |
19 |
0.38 |
|
B |
75-89 |
m |
x |
|
C |
60-74 |
n |
y |
|
D |
60以下 |
3 |
0.06 |
|
合计 |
|
50 |
1.00 |
请你根据以上图表提供的信息,解答下列问题:
(1)m= 20 ,n= 8 ,x= 0.4 ,y= 0.16 ;
(2)在扇形图中,C等级所对应的圆心角是 57.6 度;
(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
考点:频数(率)分布表;用样本估计总体;扇形统计图。
专题:图表型。
分析:(1)让总人数50乘以相应的百分比40%可得m的值,x为相应百分比;让总人数50减去其余已知人数可得n的值,除以50即为y的值;
(2)让360乘以相应频率即为C等级所对应的圆心角;
(3)让总人数35000乘以AB两个等级的百分比的和即为所求的人数.
解答:解:(1)50×40%=20,0.4;50﹣19﹣20﹣3=8,8÷50=0.16;
故答案为:20,8,0.4,0.16(4分)
(2)0.16×360=57.6°,
故答案为57.6.(6分)
(3)由上表可知达到优秀和良好的共有19+20=39人,500×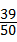 =390人.(8分)
=390人.(8分)
点评:考查有关识图问题;读懂图意是解决本题的关键;用到的知识点为:频数=总数×相应频率.
 .
.
 .
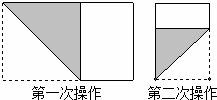
.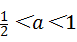 ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为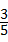 或
或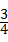 .
.
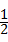 <a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1﹣a,a.由1﹣a<a可知,第二次操作时所得正方形的边长为1﹣a,剩下的矩形相邻的两边分别为1﹣a,a﹣(1﹣a)=2a﹣1.由于(1﹣a)﹣(2a﹣1)=2﹣3a,所以(1﹣a)与(2a﹣1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
<a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1﹣a,a.由1﹣a<a可知,第二次操作时所得正方形的边长为1﹣a,剩下的矩形相邻的两边分别为1﹣a,a﹣(1﹣a)=2a﹣1.由于(1﹣a)﹣(2a﹣1)=2﹣3a,所以(1﹣a)与(2a﹣1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.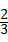 ,那么第三次操作时正方形的边长为2a﹣1.
,那么第三次操作时正方形的边长为2a﹣1.
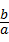 =﹣
=﹣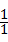 =﹣1,x1•x2=
=﹣1,x1•x2=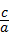 =
=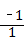 =﹣1,
=﹣1,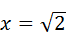 时,
时,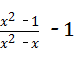 =
=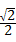 .
.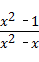 ﹣1
﹣1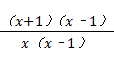 ﹣1
﹣1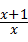 ﹣
﹣
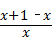
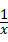 ,将x=
,将x=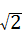 代入上式中得,
代入上式中得,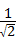 =
=