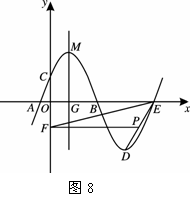
摘要:解: (1)设线段与轴的交点为.由抛物线的对称性可得为中点. .. .(.) --- 2分 将(.)代入抛物线得.. --- 3分 (2)解法一:过点作轴于点. 点的横坐标为. (1.). --- 4分 . 又 .易知.又. △∽△. --- 5分 设点(.)().则.. .即点的横坐标为. --- 6分 解法二:过点作轴于点. 点的横坐标为. (1.). --- 4分 .易知. . --- 5分 设点(-.)().则.. .即点的横坐标为. --- 6分 解法三:过点作轴于点. 点的横坐标为. (1.). --- 4分 设(-.)().则 ... . . 解得:.即点的横坐标为. --- 6分 (3)解法一:设(.)().(.)(). 设直线的解析式为:. 则.--- 7分 得.. --- 8分 又易知△∽△...--- 9分 .由此可知不论为何值.直线恒过点(.)---10分 (说明:写出定点的坐标就给2分) 解法二:设(.)().(.)(). 直线与轴的交点为.根据.可得 . 化简.得. --- 8分 又易知△∽△...--- 9分为固定值.故直线恒过其与轴的交点(,)--- 10分 说明:的值也可以通过以下方法求得. 由前可知.... 由.得:. 化简.得. 本答案仅供参考.若有其他解法.请参照本评分标准 26.如图.在Rt△ABC中.∠ACB=90°.AC=6㎝.BC=8㎝.P为BC的中点.动点Q从点P出发.沿射线PC方向以2㎝/s的速度运动.以P为圆心.PQ长为半径作圆.设点Q运动的时间为t s. ⑴当t=1.2时.判断直线AB与⊙P的位置关系.并说明理由, ⑵已知⊙O为△ABC的外接圆.若⊙P与⊙O相切.求t的值. 27.如图①.P为△ABC内一点.连接PA.PB.PC.在△PAB.△PBC和△PAC中.如果存在一个三角形与△ABC相似.那么就称P为△ABC的自相似点. ⑴如图②.已知Rt△ABC中.∠ACB=90°.∠ACB>∠A.CD是AB上的中线.过点B作BE⊥CD.垂足为E.试说明E是△ABC的自相似点. ⑵在△ABC中.∠A<∠B<∠C. ①如图③.利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹), ②若△ABC的内心P是该三角形的自相似点.求该三角形三个内角的度数. 28. 问题情境 已知矩形的面积为a(a为常数.a>0).当该矩形的长为多少时.它的周长最小?最小值是多少? 数学模型 设该矩形的长为x.周长为y.则y与x的函数关系式为. 探索研究 ⑴我们可以借鉴以前研究函数的经验.先探索函数的图象性质. ① 填写下表.画出函数的图象: ② x -- 1 2 3 4 -- y -- -- ②观察图象.写出该函数两条不同类型的性质, ③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时.除了通过观察图象.还可以通过配方得到.请你通过配方求函数的最小值. 解决问题 ⑵用上述方法解决“问题情境 中的问题.直接写出答案.
网址:http://m.1010jiajiao.com/timu3_id_495311[举报]
解:(1)A(-1,0),B(3,0),C(0,3).·················· 2分
抛物线的对称轴是:x=1.······················· 3分
 (2)①设直线BC的函数关系式为:y=kx+b.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
![]() 解得:k= -1,b=3.
解得:k= -1,b=3.
所以直线BC的函数关系式为:![]() .
.
当x=1时,y= -1+3=2,∴E(1,2).
当![]() 时,
时,![]() ,
,
∴P(m,![]() m+3).·························· 4分
m+3).·························· 4分
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]() ∴
∴![]() ········· 5分
········· 5分
∴线段DE=4-2=2,线段![]() ···· 6分
···· 6分
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
由![]() 解得:
解得:![]() (不合题意,舍去).
(不合题意,舍去).
因此,当![]() 时,四边形
时,四边形![]() 为平行四边形.··········· 7分
为平行四边形.··········· 7分
②设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,由
,由![]() 可得:
可得:![]()
∵![]() ························ 8分
························ 8分
即![]() .
.
![]()
![]() ·········· 9分
·········· 9分
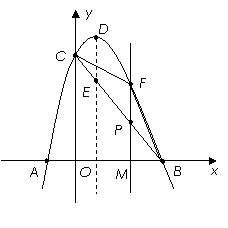
如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标为(8、0),tan∠ABC=
,△ABC的面积为8,
(1)求:抛物线的解析式;
(2)若动直线EF(EF∥x轴),从C点开始,以每秒1个长度单位的速度向X轴方向平移,与x轴重合时结束,并且分别交y轴、线段CB于E、F两点.动点P同时从B点出发在线段OB上以每秒2个长度单位的速度向原点O运动,运动到O点结束,连接FP,设运动时间为t秒,是否存在t的值,使以P、B、F为顶点的三角形与△ABC相似?若存在,请求出t的值;若不存在,请说明理由.
(3)在(2)的条件下,设AC与EF交于点M,求当t为何值时,M、P、A、F所围成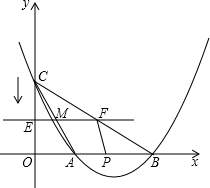 的图形是平行四边形、等腰梯形和等腰直角三角形?
查看习题详情和答案>>
的图形是平行四边形、等腰梯形和等腰直角三角形?
查看习题详情和答案>>
| 1 | 2 |
(1)求:抛物线的解析式;
(2)若动直线EF(EF∥x轴),从C点开始,以每秒1个长度单位的速度向X轴方向平移,与x轴重合时结束,并且分别交y轴、线段CB于E、F两点.动点P同时从B点出发在线段OB上以每秒2个长度单位的速度向原点O运动,运动到O点结束,连接FP,设运动时间为t秒,是否存在t的值,使以P、B、F为顶点的三角形与△ABC相似?若存在,请求出t的值;若不存在,请说明理由.
(3)在(2)的条件下,设AC与EF交于点M,求当t为何值时,M、P、A、F所围成
 的图形是平行四边形、等腰梯形和等腰直角三角形?
查看习题详情和答案>>
的图形是平行四边形、等腰梯形和等腰直角三角形?
查看习题详情和答案>>
如图,抛物线y=﹣x2+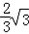 x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
(1)分别求出点A.点B的坐标;
(2)求直线AB的解析式;
(3)若反比例函数y= 的图象过点D,求k值;
的图象过点D,求k值;
(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
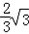 x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.(1)分别求出点A.点B的坐标;
(2)求直线AB的解析式;
(3)若反比例函数y=
 的图象过点D,求k值;
的图象过点D,求k值;(4)两动点P、Q同时从点A出发,分别沿AB.AO方向向B.O移动,点P每秒移动1个单位,点Q每秒移动
 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.