17. (2011江苏泰州,21,8分)一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,请用树状图或列表的方法列出所有可能的结果,写出两次摸出的球颜色相同的概率.
[答案]解:(1)树状图: 列表法:
|
2次 1次 |
红 |
白 |
白 |
|
红 |
(红,红) |
(红,白) |
(红,白) |
|
白 |
(白,红) |
(白,白) |
(白,白) |
|
白 |
(白,红) |
(白,白) |
(白,白) |


所有可能的结果如图所示,两次摸出的球颜色相同的概率为 .
.
16. (2011江苏宿迁,24,10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
[答案]
解:(1)∵
|
|
1 |
2 |
3 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)= =
= .
.
(3)∵
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
4 |
|
2 |
3 |
4 |
5 |
|
3 |
4 |
5 |
6 |
∴P(点M的横坐标与纵坐标之和是偶数)= .
.
11. (2011福建泉州,22,9分)在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数 的图象上的概率;
的图象上的概率;
(3)求小明、小华各取一次小球所确定的数x、y满足 的概率.
的概率.
[答案]解:(1)
 x xy |
1 |
2 |
3 |
4 |
|
1 |
(1,1) |
(2,1) |
(3,1) |
(4,1) |
|
2 |
(1,2) |
(2,2) |
(3,2) |
(4,2) |
|
3 |
(1,3) |
(2,3) |
(3,3) |
(4,3) |
|
4 |
(1,4) |
(2,4) |
(3,4) |
(4,4) |
······························································································································································ 3分
(2)可能出现的结果共有16个,它们出现的可能性相等.·········································· 4分
满足点(x,y)落在反比例函数 的图象上(记为事件A)的结果有3个,即(1,4),(2,2),
的图象上(记为事件A)的结果有3个,即(1,4),(2,2),
(4,1),
所以P(A)= .·································································································································· 7分
.·································································································································· 7分
(3)能使x,y满足 (记为事件B)的结果有5个,即(1,1),(1,2),(1,3),(2,1),(3,1),所以P(B)=
(记为事件B)的结果有5个,即(1,1),(1,2),(1,3),(2,1),(3,1),所以P(B)= 9分
9分
10.(2011江西,18,6分)甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛,
⑴请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
⑵若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率。
[答案](1)列表法如下:
|
|
甲 |
乙 |
丙 |
丁 |
|
甲 |
|
乙甲 |
丙甲 |
丁甲 |
|
乙 |
甲乙 |
|
丙乙 |
丁乙 |
|
丙 |
甲丙 |
乙丙 |
|
乙丙 |
|
丁 |
甲丙 |
乙丁 |
丙丁 |
|
所有可能出现的情况有12种,其中甲乙两位同学组合的情况有两种,
所以P(甲乙)= =
= .
.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,共有3种情况选中乙的情况有一种,所以P(恰好选中乙同学)= .
.
9. (2011四川重庆,23,10分)为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:
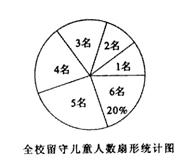
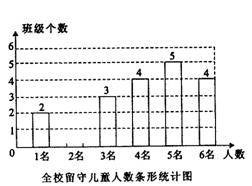
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
[答案](1)4÷20﹪=20(个);20-2-3-4-5-4=2(个),
(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(名).
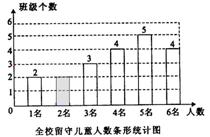
答:该校平均每班有4名留守儿童.
(2)因为只有2名留守儿童的班级只有甲班和乙班两个,设甲班的2名留守儿童为a1,a2,乙班的2名留守儿童为b1,b2,列表如下:
|
|
a1 |
a2 |
b1 |
b2 |
|
a1 |
|
a1a2 |
a1b1 |
a1b2 |
|
a2 |
a1 a2 |
|
a2b1 |
a2b2 |
|
b1 |
a1 b1 |
a2 b1 |
|
b1b2 |
|
b2 |
a1 b2 |
a2 b2 |
b1 b2 |
|
由表格可知:共有12种情况,符合条件的有a1 a2、a1a2、b1 b2、b1b2四种,4÷12=.
答:所选两名留守儿童来自同一个班级的概率为.
 个蓝球,则从乙盒中任意摸取一球,摸到蓝球的概率
个蓝球,则从乙盒中任意摸取一球,摸到蓝球的概率 ;
; ;
; ,
, ,所以乙盒中有3个蓝球.
,所以乙盒中有3个蓝球.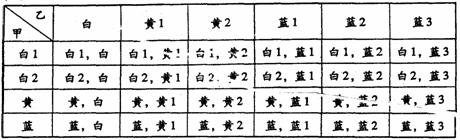
 .
. .
. ,从乙盒中任意摸取一球,摸到蓝球的概率为
,从乙盒中任意摸取一球,摸到蓝球的概率为 .
. .
.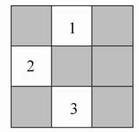
 =
= .
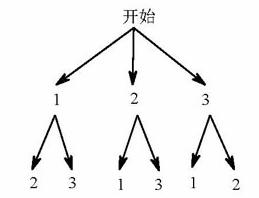
.
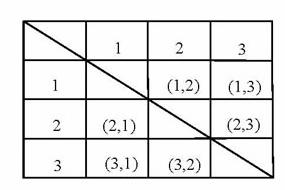
 =
=
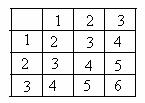
 .
. ,解得x=1.
,解得x=1.

 (从中摸出两个得2分)=
(从中摸出两个得2分)= .
.

 2
4
6
2
4
6 ,乙获胜的概率为
,乙获胜的概率为