摘要：解⑴直线与⊙P相切． 如图.过点P作PD⊥AB, 垂足为D． 在Rt△ABC中.∠ACB＝90°.∵AC=6cm.BC=8cm. ∴．∵P为BC的中点.∴PB=4cm． ∵∠PDB＝∠ACB＝90°.∠PBD＝∠ABC．∴△PBD∽△ABC． ∴,即.∴PD =2.4(cm) ． 当时.(cm) ∴.即圆心到直线的距离等于⊙P的半径． ∴直线与⊙P相切． ⑵ ∠ACB＝90°.∴AB为△ABC的外切圆的直径．∴． 连接OP．∵P为BC的中点.∴． ∵点P在⊙O内部.∴⊙P与⊙O只能内切． ∴或.∴=1或4． ∴⊙P与⊙O相切时.t的值为1或4．
网址：http://m.1010jiajiao.com/timu3_id_495312[举报]
如图，在平面直角坐标系中的正方形ABCD的边长为acm（a＞2），B与坐标原点重合，边AB在y轴正半轴，动点P从点B出发，以2cm/s的速度沿B→C→D方向，向点D运动；动点Q从点A出发，以1cm/s的速度沿A→B方向，向点B运动，设P，Q两点同时出发，运动时间为ts．
（1）若t=1时，△BPQ的面积为3cm2，则a的值为多少？
（2）在（1）的条件下，以点P为圆心，作⊙P，使得⊙P与对角线BD相切如图（b）所示，问：当点P在CD上动动时，是否存在这样的t，使得⊙P恰好经过正方形ABCD的某一边的中点？若存在，请写出符合条件的t的值并直接写出直线PQ解析式（其中一种情形需有计算过程，其余的只要直接写出答案）；若不存在，请说明理由．
（3）在（1）的条件下，且t＜
，点P在BC上运动时，△PQD是以PD为一腰的等腰三角形，在直线BD上找一点E，在x轴上找一点F，是否存在以E，F，P，Q为顶点的平行四边形？若存在，求出E，F两点坐标；若不存在，请说明理由．
查看习题详情和答案>>
（1）若t=1时，△BPQ的面积为3cm2，则a的值为多少？
（2）在（1）的条件下，以点P为圆心，作⊙P，使得⊙P与对角线BD相切如图（b）所示，问：当点P在CD上动动时，是否存在这样的t，使得⊙P恰好经过正方形ABCD的某一边的中点？若存在，请写出符合条件的t的值并直接写出直线PQ解析式（其中一种情形需有计算过程，其余的只要直接写出答案）；若不存在，请说明理由．
（3）在（1）的条件下，且t＜
| 3 | 2 |
如图，在平面直角坐标系中的正方形ABCD的边长为acm（a＞2），B与坐标原点重合，边AB在y轴正半轴，动点P从点B出发，以2cm/s的速度沿B→C→D方向，向点D运动；动点Q从点A出发，以1cm/s的速度沿A→B方向，向点B运动，设P，Q两点同时出发，运动时间为ts．
（1）若t=1时，△BPQ的面积为3cm2，则a的值为多少？
（2）在（1）的条件下，以点P为圆心，作⊙P，使得⊙P与对角线BD相切如图（b）所示，问：当点P在CD上动动时，是否存在这样的t，使得⊙P恰好经过正方形ABCD的某一边的中点？若存在，请写出符合条件的t的值并直接写出直线PQ解析式（其中一种情形需有计算过程，其余的只要直接写出答案）；若不存在，请说明理由．
（3）在（1）的条件下，且
，点P在BC上运动时，△PQD是以PD为一腰的等腰三角形，在直线BD上找一点E，在x轴上找一点F，是否存在以E，F，P，Q为顶点的平行四边形？若存在，求出E，F两点坐标；若不存在，请说明理由．
查看习题详情和答案>>
（1）若t=1时，△BPQ的面积为3cm2，则a的值为多少？
（2）在（1）的条件下，以点P为圆心，作⊙P，使得⊙P与对角线BD相切如图（b）所示，问：当点P在CD上动动时，是否存在这样的t，使得⊙P恰好经过正方形ABCD的某一边的中点？若存在，请写出符合条件的t的值并直接写出直线PQ解析式（其中一种情形需有计算过程，其余的只要直接写出答案）；若不存在，请说明理由．
（3）在（1）的条件下，且
，点P在BC上运动时，△PQD是以PD为一腰的等腰三角形，在直线BD上找一点E，在x轴上找一点F，是否存在以E，F，P，Q为顶点的平行四边形？若存在，求出E，F两点坐标；若不存在，请说明理由．查看习题详情和答案>>
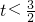，点P在BC上运动时，△PQD是以PD为一腰的等腰三角形，在直线BD上找一点E，在x轴上找一点F，是否存在以E，F，P，Q为顶点的平行四边形？若存在，求出E，F两点坐标；若不存在，请说明理由．
不存在，请说明理由．
不存在，请说明理由．