24、(2011•泰安)甲、乙两人在5次体育测试中的成绩(成绩为整数,满分为100分)如下表,其中乙的第5次成绩的个位数被污损.
|
|
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
|
甲 |
90 |
88 |
87 |
93 |
92 |
|
乙 |
84 |
87 |
85 |
98 |
9■ |
则乙的平均成绩高于甲的平均成绩的概率是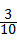 .
.
考点:概率公式;算术平均数。
专题:应用题。
分析:首先计算出甲的平均成绩,再根据乙的成绩在97,98,99的时候,平均成绩大于甲的成绩,随机事件概率的求法即可得出结果.
解答:解:甲的平均成绩为: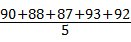 =90,
=90,
乙的被污损的成绩可能是90,91,92,93,94,95,96,97,98,99共10中可能,
乙的成绩为97,98,99的时候,平均成绩大于甲的成绩,
乙的平均成绩高于甲的平均成绩的概率是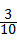 .
.
故答案为: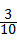 .
.
点评:本题考查了平均数的求法,以及随机事件概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=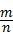 ,难度适中.
,难度适中.
 C.(a2)3=a6
D.(a+b)2=a2+b2
C.(a2)3=a6
D.(a+b)2=a2+b2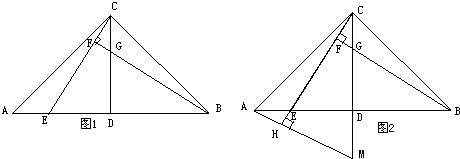
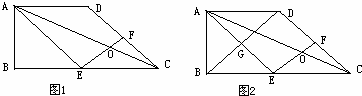
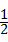 BC=AD,
BC=AD, (2)证明:连接DE,
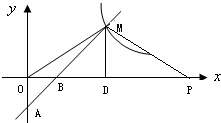
(2)证明:连接DE,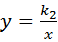 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.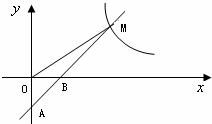
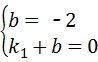 ,
,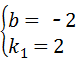
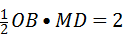 ,
,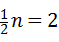
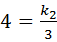 ,
,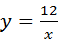
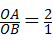 =2(8分)
=2(8分)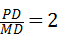 ,
,
 ,
,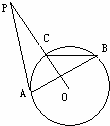
 连接OA.
连接OA.