摘要:已知:在△ABC中.AC=BC.∠ACB=90°.点D是AB的中点.点E是AB边上一点. (1)直线BF垂直于直线CE于点F.交CD于点G.求证:AE=CG, (2)直线AH垂直于直线CE.垂足为点H.交CD的延长线于点M.找出图中与BE相等的线段.并证明. 考点:全等三角形的判定与性质,等腰直角三角形. 专题:证明题. 分析:(1)首先根据点D是AB中点.∠ACB=90°.可得出∠ACD=∠BCD=45°.判断出△AEC≌△CGB.即可得出AE=CG. (2)根据垂直的定义得出∠CMA+∠MCH=90°.∠BEC+∠MCH=90°.再根据AC=BC.∠ACM=∠CBE=45°.得出△BCE≌△CAM.进而证明出BE=CM. 解答:解:(1)证明:∵点D是AB中点.AC=BC.∠ACB=90°. ∴CD⊥AB.∠ACD=∠BCD=45°. ∴∠CAD=∠CBD=45°. ∴∠CAE=∠BCG.又BF⊥CE. ∴∠CBG+∠BCF=90°.又∠ACE+∠BCF=90°. ∴∠ACE=∠CBG. ∴△AEC≌△CGB. ∴AE=CG. (2)BE=CM. 证明:∵CH⊥HM.CD⊥ED. ∴∠CMA+∠MCH=90°.∠BEC+∠MCH=90°. ∴∠CMA=∠BEC. 又∵AC=BC.∠ACM=∠CBE=45°. ∴△BCE≌△CAM. ∴BE=CM. 点评:本题主要考查了全等三角形的判定方法以及全等三角形对应边相等的性质.难度适中.
网址:http://m.1010jiajiao.com/timu3_id_494808[举报]
已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,
∠ABE=∠DBM.
(1)如图1,当∠ABC=45°时,求证:AE=
MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=2
,求tan∠PCB和tan∠ACP的值.

查看习题详情和答案>>
∠ABE=∠DBM.
(1)如图1,当∠ABC=45°时,求证:AE=
| 2 |
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为
AE=2MD
AE=2MD
;(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=2
| 7 |

已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)如图1,当∠ABC=45°时,求证:AE=
MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: .
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=2
,求tan∠ACP的值.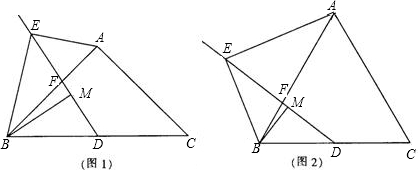 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图1,当∠ABC=45°时,求证:AE=
| 2 |
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为:
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=2
| 7 |
 查看习题详情和答案>>
查看习题详情和答案>>
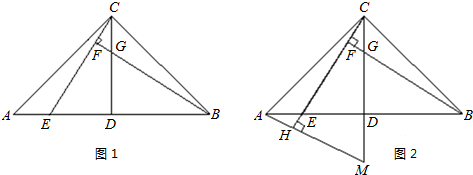
已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)求证:△ACD≌△BCD;
(2)求∠A;
(3)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(4)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.

查看习题详情和答案>>
(1)求证:△ACD≌△BCD;
(2)求∠A;
(3)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(4)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.

 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上.