摘要:如图.一次函数y=k1x+b的图象经过A两点.与反比例函数的图象在第一象限内的交点为M.若△OBM的面积为2. (1)求一次函数和反比例函数的表达式, (2)在x轴上是否存在点P.使AM⊥MP?若存在.求出点P的坐标,若不存在.说明理由. 考点:反比例函数与一次函数的交点问题. 专题:探究型. 分析:(1)根据一次函数y=k1x+b的图象经过A可得到关于b.k1的方程组.进而可得到一次函数的解析式.设M(m.n)作MD⊥x轴于点D.由△OBM的面积为2可求出n的值.将M(m.4)代入y=2x﹣2求出m的值.由M(3.4)在双曲线上即可求出k2的值.进而求出其反比例函数的解析式, 作MP⊥AM交x轴于点P.由MD⊥BP可求出∠PMD=∠MBD=∠ABO.再由锐角三角函数的定义可得出OP的值.进而可得出结论. 解答:(1)∵直线y=k1x+b过A两点 ∴. ∴ ∴已知函数的表达式为y=2x﹣2. ∴设M(m.n)作MD⊥x轴于点D ∵S△OBM=2. ∴. ∴ ∴n=4 ∴将M(m.4)代入y=2x﹣2得4=2m﹣2. ∴m=3 ∵M(3.4)在双曲线上. ∴. ∴k2=12 ∴反比例函数的表达式为 作MP⊥AM交x轴于点P. ∵MD⊥BP. ∴∠PMD=∠MBD=∠ABO ∴tan∠PMD=tan∠MBD=tan∠ABO==2 ∴在Rt△PDM中.. ∴PD=2MD=8. ∴OP=OD+PD=11 ∴在x轴上存在点P.使PM⊥AM.此时点P的坐标为 点评:本题考查的是反比例函数与一次函数的交点问题.涉及到的知识点为用待定系数法求一次函数与反比例函数的解析式.锐角三角函数的定义.熟知以上知识是解答此题的关键.
网址:http://m.1010jiajiao.com/timu3_id_494805[举报]
 如图,一次函数y=k1x+b与反比例函数y=
如图,一次函数y=k1x+b与反比例函数y=| k2 |
| x |
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>
| k2 |
| x |
(3)若P(p,y1),Q(-2,y2)是函数y=
| k2 |
| x |
如图,一次函数y1=k1x+2与反比例函数y2=
的图象交于点A(4,m)和B(-8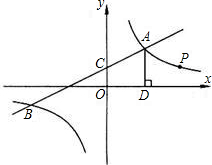 ,-2),与y轴交于点C.
,-2),与y轴交于点C.
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标. 查看习题详情和答案>>
| k2 | x |
 ,-2),与y轴交于点C.
,-2),与y轴交于点C.(1)k1=
(2)根据函数图象可知,当y1>y2时,x的取值范围是
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标. 查看习题详情和答案>>
 如图,一次函数y1=k1x+b的图象和反比例函数y2=
如图,一次函数y1=k1x+b的图象和反比例函数y2=| k2 |
| x |
| A、x<1 |
| B、x<-2 |
| C、-2<x<0或x>1 |
| D、x<-2或0<x<1 |
 如图,一次函数y1=k1x+2与反比例函数
如图,一次函数y1=k1x+2与反比例函数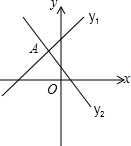 如图,一次函数y1=k1x+b1与y2=k2x+b2交于点A
如图,一次函数y1=k1x+b1与y2=k2x+b2交于点A