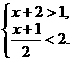24.(本题满分10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
解:(1)∵
|
|
1 |
2 |
3 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)=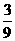 =
=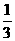 .
.
(3)∵
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
4 |
|
2 |
3 |
4 |
5 |
|
3 |
4 |
5 |
6 |
∴P(点M的横坐标与纵坐标之和是偶数)=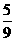 .
.
22.(本题满分8分)省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
|
|
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
|
甲 |
10 |
8 |
9 |
8 |
10 |
9 |
|
乙 |
10 |
7 |
10 |
10 |
9 |
8 |
(1)根据表格中的数据,计算出甲的平均成绩是 ▲ 环,乙的平均成绩是 ▲ 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=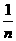 [
[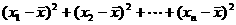 ])
])
解:(1)9;9.
(2)s2甲=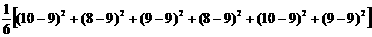
=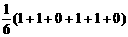 =
=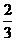 ;
;
s2乙=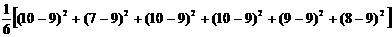
=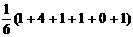 =
=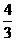 .
.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
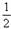 D、
D、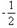
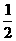 ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.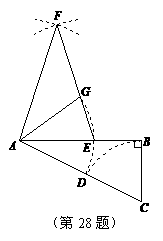 (2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.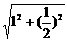 =
=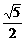
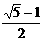 .
.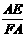 =
=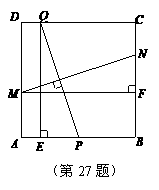 (本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.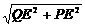 =
=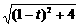
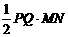 =
=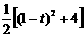 =
=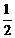 t2-t+
t2-t+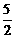
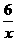 (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.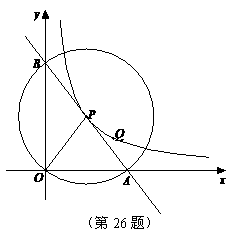 ∵点O在⊙P上,且∠AOB=90°
∵点O在⊙P上,且∠AOB=90°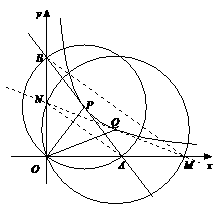 (3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
(3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.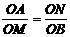
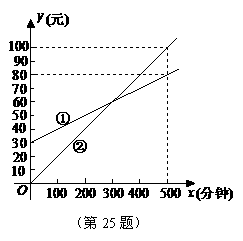 (3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.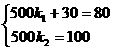 ,解得
,解得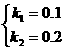
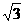 =1.732,结果精确到1m)
=1.732,结果精确到1m)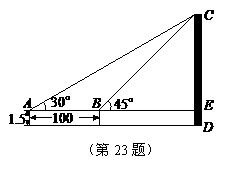
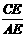 ,即tan30°=
,即tan30°=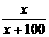
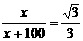 ,3x=
,3x=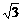 (x+100)
(x+100)