0 49300 49308 49314 49318 49324 49326 49330 49336 49338 49344 49350 49354 49356 49360 49366 49368 49374 49378 49380 49384 49386 49390 49392 49394 49395 49396 49398 49399 49400 49402 49404 49408 49410 49414 49416 49420 49426 49428 49434 49438 49440 49444 49450 49456 49458 49464 49468 49470 49476 49480 49486 49494 447348
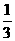
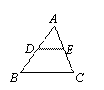 A.3
B.-3
C.-
D.
A.3
B.-3
C.-
D.  (B)
(B)
 (D)
(D)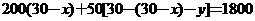
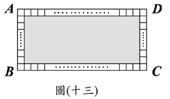 (D)31. 如图(十三),将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形。根据右图,若灰色长方形之长与宽的比为5:3,则
(D)31. 如图(十三),将长方形ABCD分割成1个灰色长方形与148个面积相等的小正方形。根据右图,若灰色长方形之长与宽的比为5:3,则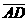 :
: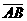 =?
=?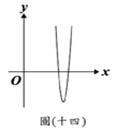 (A)32. 如图(十四),将二次函数
(A)32. 如图(十四),将二次函数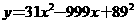 的图形画在坐标平面上,判断方程式
的图形画在坐标平面上,判断方程式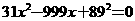 的两根,下列叙述何者正确?
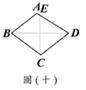
的两根,下列叙述何者正确? (D)33. 图(十五)为一个四边形
(D)33. 图(十五)为一个四边形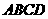 ,其中
,其中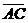 与
与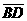 交于E点,且两灰色区域的面积相等。若
交于E点,且两灰色区域的面积相等。若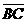 =10,则下列关系何者正确?
=10,则下列关系何者正确?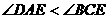
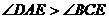
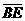 >
>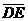
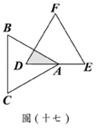
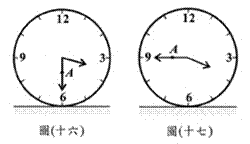 (D)34. 图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分?
(D)34. 图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分?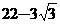 (B)
(B)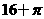 (C)18(D)19
(C)18(D)19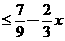 ,得其解的范围为何?
,得其解的范围为何?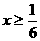 (B)
(B)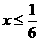 (C)
(C)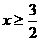 (D)
(D)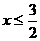
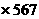 3=103,a
3=103,a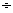 103=b,则
103=b,则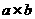 之值为何?
之值为何?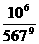 (B)
(B)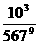 (C)
(C)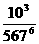 (D)
(D)
 的两根为0、2,则
的两根为0、2,则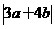 之值为何?(A) 2 (B) 5 (C) 7 (D) 8
之值为何?(A) 2 (B) 5 (C) 7 (D) 8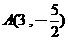 、
、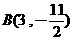 两点在此图形上且互为对称点。若此图形上有一点
两点在此图形上且互为对称点。若此图形上有一点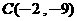 ,则C的对称点坐标为何?
,则C的对称点坐标为何?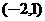 (B)
(B)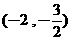 (C)
(C)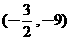 (D)
(D)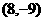
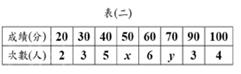 (B)22. 表(二)为某班成绩的次数分配表。已知全班共有38人,且众数为50分,中位数为60分,求
(B)22. 表(二)为某班成绩的次数分配表。已知全班共有38人,且众数为50分,中位数为60分,求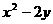 之值为何?
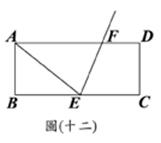
之值为何? (B)23. 如图(八),三边均不等长的
(B)23. 如图(八),三边均不等长的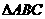 ,若在此三角形内找一点O,使得
,若在此三角形内找一点O,使得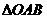 、
、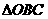 、
、 的面积均相等。判断下列作法何者正确?
的面积均相等。判断下列作法何者正确?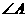 、
、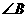 的角平分线,再取此两角平分线的交点O
的角平分线,再取此两角平分线的交点O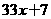 的倍式?
的倍式?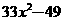 (B)
(B)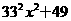 (C)
(C)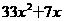 (D)
(D)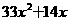
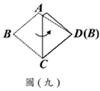
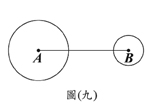 (B)25. 如图(九),圆A、圆B的半径分别为4、2,且
(B)25. 如图(九),圆A、圆B的半径分别为4、2,且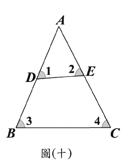 (C)
5 (D) 6
(C)
5 (D) 6 =29,
=29,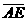 =30,
=30,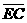 =32。若
=32。若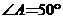 ,则图中
,则图中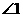 、
、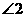 、
、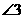 、
、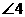 的大小关系,下列何者正确?
的大小关系,下列何者正确?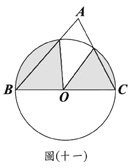 (D)27. 图(十一)为
(D)27. 图(十一)为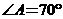 ,
,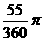 (B)
(B)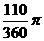
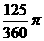 (D)
(D)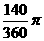
 (A)
136 (B) 192 (C) 240 (D) 544
(A)
136 (B) 192 (C) 240 (D) 544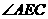 的角平分线交
的角平分线交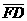 的长度为何?
的长度为何?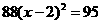 的兩根,下列判斷何者正確?
的兩根,下列判斷何者正確?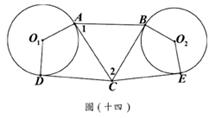 (A)32. 圖(十四)中,
(A)32. 圖(十四)中,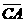 、
、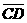 分別切圓O1於A、D兩點,
分別切圓O1於A、D兩點, 、
、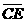 分別切圓O2於B、E兩點。
若∠1=60∘,∠2=65∘,判斷
分別切圓O2於B、E兩點。
若∠1=60∘,∠2=65∘,判斷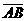 、
、
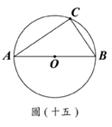 (D)33. 如圖(十五),
(D)33. 如圖(十五),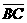 、
、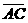 。若想在
。若想在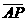 長,判斷下列四個作法何者正確?
長,判斷下列四個作法何者正確?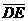 上,如圖(十七)所示。求圖(十六)與圖(十七)中,兩個三角形重疊區域的面積比為何?
上,如圖(十七)所示。求圖(十六)與圖(十七)中,兩個三角形重疊區域的面積比為何?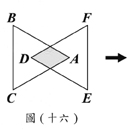
 ,如圖(八)。將B點摺向D,使得B、D兩點重疊,如圖(九),展開後出現摺線
,如圖(八)。將B點摺向D,使得B、D兩點重疊,如圖(九),展開後出現摺線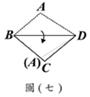
 //
//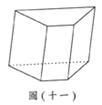 (C)27. 圖(十一)為一直角柱,其中兩底面為全等的梯形,其面積和為16;四個側面均為長方形,其面積和為45。若此直角柱的體積為24,則所有邊的長度和為何?
(C)27. 圖(十一)為一直角柱,其中兩底面為全等的梯形,其面積和為16;四個側面均為長方形,其面積和為45。若此直角柱的體積為24,則所有邊的長度和為何?  (D)28. 圖(十二)為座標平面上二次函數
(D)28. 圖(十二)為座標平面上二次函數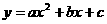 的圖形,且此圖形通
(-1 , 1)、(2 ,-1)兩點。下列關於此二次函數的敘述,何者正確?
的圖形,且此圖形通
(-1 , 1)、(2 ,-1)兩點。下列關於此二次函數的敘述,何者正確?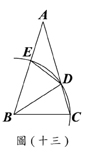 (C)30. 如圖(十三),ΔABC中,以B為圓心,
(C)30. 如圖(十三),ΔABC中,以B為圓心,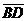 、
、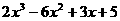 除以(x-2)2後,得餘式為何?
除以(x-2)2後,得餘式為何?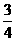
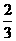
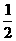
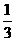
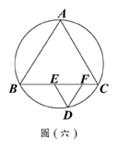 (C)24. 如圖(六),△ABC的外接圓上,AB、BC、CA三弧的度數比為12:13:11。自BC上取一點D,過D分別作直線AC、直線AB的平行線,且交
(C)24. 如圖(六),△ABC的外接圓上,AB、BC、CA三弧的度數比為12:13:11。自BC上取一點D,過D分別作直線AC、直線AB的平行線,且交 (A) 20
(A) 20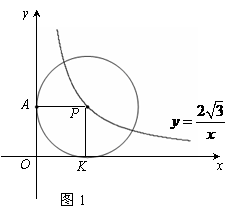 (本题满分12分)
(本题满分12分)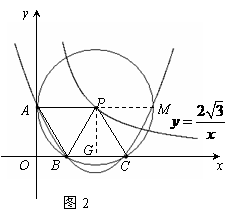 (2)①连接PB,设点P的横坐标为x,则其纵坐标为
(2)①连接PB,设点P的横坐标为x,则其纵坐标为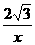 .
.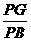 ,即
,即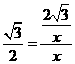 .
.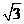 ,PA=BC=2.……………………4分
,PA=BC=2.……………………4分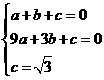
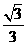 , b=
, b=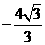 , c=
, c=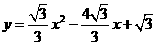 .……………………9分
.……………………9分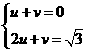
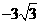 .
.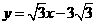 .
.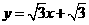 .
.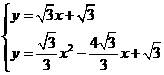
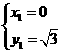 ;
; 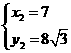 .
.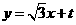 .
.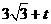 .
. 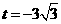 .
.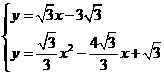
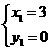 ;
; 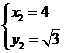 .
.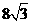 ).…………………12分
).…………………12分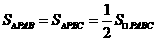 ,
,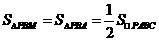 .
.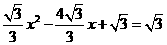 .
.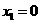 (舍),
(舍),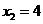 .
.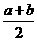 >
>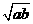 ,
, 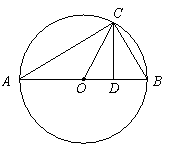 ●探究证明:
●探究证明: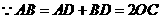 ,
,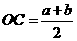 …………………3分
…………………3分 AB为⊙O直径,
AB为⊙O直径,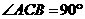 .
.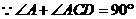 ,
,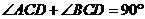 ,
, ∽△
∽△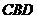 . …………………4分
. …………………4分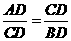 .
.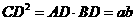 ,
, .
…………………5分
.
…………………5分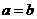 时,
时,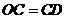 ,
, 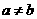 时,
时,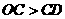 ,
, 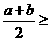
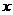 米,则另一边长为
米,则另一边长为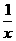 米,设镜框周长为l米,则
米,设镜框周长为l米,则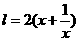 ≥
≥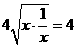 .
……………9分
.
……………9分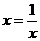 ,即
,即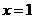 (米)时,镜框周长最小.
(米)时,镜框周长最小.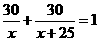 . ………………………………3分
. ………………………………3分