21.(本题满分8分)小明有3支水笔,分别为红色、蓝色、黑色;有2块橡皮,分别为
白色、灰色.小明从中任意取出1支水笔和1块橡皮配套使用.试用树状图或表格列出所有
可能的结果,并求取出红色水笔和白色橡皮配套的概率.
[答案]解:解法一:画树状图:
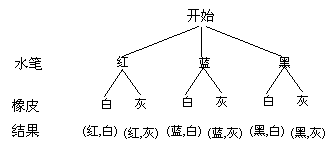
P(红色水笔和白色橡皮配套)= .
解法二:用列表法:
|
白 |
灰 |
||||||
|
红 |
(红,白) |
(红,灰) |
||||||
|
蓝 |
(蓝,白) |
(蓝,灰) |
||||||
|
黑 |
(黑,白) |
(黑,灰) |
P(红色水笔和白色橡皮配套)= .
[考点]概率,树状图或列表法。
[分析]用树状图或列表法列举出所有情况,并找取出红色水笔和白色橡皮配套的情况数,求出概率.
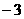 的倒数为( )
的倒数为( )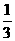 C.
C.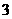 D.
D. 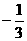
 (本题满分12分)如图,已知一次函数y = -
x +7与正比例函数y = x的图象交于点A,
(本题满分12分)如图,已知一次函数y = -
x +7与正比例函数y = x的图象交于点A,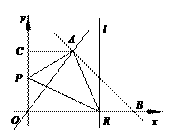 存在,请说明理由.
存在,请说明理由.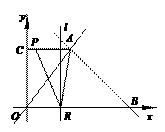 (3+7)×4-×3×(4-t)- t(7-t)-
t×4=8
(3+7)×4-×3×(4-t)- t(7-t)-
t×4=8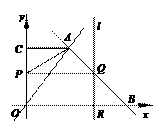 当P在CA上运动时,4≤t<7. 此时直线l交AO于Q。过A作AD⊥OB于D,则AD=BD=4.
当P在CA上运动时,4≤t<7. 此时直线l交AO于Q。过A作AD⊥OB于D,则AD=BD=4.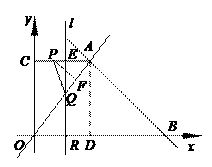 当AP=AQ时,7-t = (t-4),解得t = .
当AP=AQ时,7-t = (t-4),解得t = .
 (本题满分12分)情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是
▲ ,∠CAC′= ▲
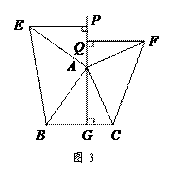
°.问题探究如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
(本题满分12分)情境观察将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是
▲ ,∠CAC′= ▲
°.问题探究如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.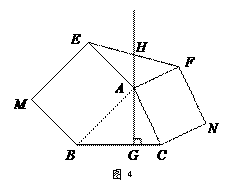 拓展延伸如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
[答案]解:情境观察
拓展延伸如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.
[答案]解:情境观察 结论: HE=HF.
结论: HE=HF.  请根据以上信息,解答下列问题:
请根据以上信息,解答下列问题:  (本题满分10分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(本题满分10分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.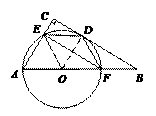
 所对的圆同角∠DEF等于圆心角∠DOB的一半,平行四边形对角相等∠DEF=∠B和直角三角形两锐角互余∠DOB+∠B=90°容易得到。
所对的圆同角∠DEF等于圆心角∠DOB的一半,平行四边形对角相等∠DEF=∠B和直角三角形两锐角互余∠DOB+∠B=90°容易得到。 (本题满分10分)如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
(本题满分10分)如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)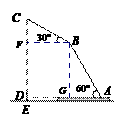 [答案]解:过点B作BF⊥CD于F,作BG⊥AD于G.
[答案]解:过点B作BF⊥CD于F,作BG⊥AD于G.  (本题满分10分)已知二次函数y = - x2 - x + .
(本题满分10分)已知二次函数y = - x2 - x + . 平移后图象所对应的函数关系式.
平移后图象所对应的函数关系式. (本题满分8分)为迎接建党90周年,某校组织了以“党在我心中”为主题的电子
(本题满分8分)为迎接建党90周年,某校组织了以“党在我心中”为主题的电子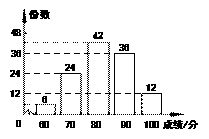
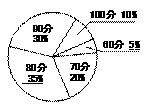 补全两幅统计图
补全两幅统计图
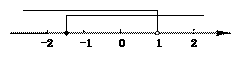 ∴原不等式组的解集是- ≤x<1.
∴原不等式组的解集是- ≤x<1.