28.(本题满分10分)十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案 (简称“个税法草案”),拟将现行个人所得税的起征点由每月2000元提高到3000元,并将9级超额累进税率修改为7级,两种征税方法的1-5级税率情况见下表:
|
税级 |
现行征税方法 |
草案征税方法 |
||||
|
月应纳税额x |
税率 |
速算扣除数 |
月应纳税额x |
税率 |
速算扣除数 |
|
|
1 |
x≤500 |
5% |
0 |
x≤1 500 |
5% |
0 |
|
2 |
500<x≤2000 |
10% |
25 |
1500<x≤4500 |
10% |
▲ |
|
3 |
2000<x≤5000 |
15% |
125 |
4500<x≤9000 |
20% |
▲ |
|
4 |
5000<x≤20000 |
20% |
375 |
9000<x≤35000 |
25% |
975 |
|
5 |
20000<x≤40000 |
25% |
1375 |
35000<x≤55 000 |
30% |
2725 |
注:“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额.
“速算扣除数”是为快捷简便计算个人所得税而设定的一个数.
例如:按现行个人所得税法的规定,某人今年3月的应纳税额为2600元,他应缴税款可以用下面两种方法之一来计算:
方法一:按1-3级超额累进税率计算,即500×5%+1500×10%十600×15%=265(元).
方法二:用“月应纳税额x适用税率一速算扣除数”计算,即2600×15%一l25=265(元)。
(1)请把表中空缺的“速算扣除数”填写完整;
(2)甲今年3月缴了个人所得税1060元,若按“个税法草案”计算,则他应缴税款多少元?
(3)乙今年3月缴了个人所得税3千多元,若按“个税法草案”计算,他应缴的税款恰好不 变,那么乙今年3月所缴税款的具体数额为多少元?
[答案]解: (1)75, 525
(2) 列出现行征税方法和草案征税方法月税额缴个人所得税y:
|
税级 |
现行征税方法月税额缴个人所得税y |
草案征税方法月税额缴个人所得税y |
|
1 |
y≤25 |
y≤75 |
|
2 |
25<y≤175 |
75<y≤375 |
|
3 |
175<y≤625 |
375<y≤1275 |
|
4 |
625<y≤3625 |
1275<y≤7775 |
|
5 |
3625<y≤8625 |
7775<y≤13775 |
因为1060元在第3税级, 所以有20%x-525=1060, x=7925(元) 答: 他应缴税款7925元.
(3)缴个人所得税3千多元的应缴税款适用第4级, 假设个人收入为k, 刚有
20%(k-2000) -375=25%(k-3000)-975 k=19000
所以乙今年3月所缴税款的具体数额为(19000-2000)×20%-375=3025(元)
[考点]统计图表的分析。
[分析](1) 当1500<x≤4500时, 应缴个人所得税为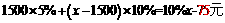
当4500<x≤9000时, 应缴个人所得税为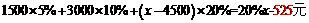
(2) 缴了个人所得税1060元, 要求应缴税款, 只要求出其适应哪一档玩税级, 直接计算即可.
(3) 同(2), 但应清楚“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额, 而“个税法草案”拟将现行个人所得税的起征点由每月2000元提高到3000元, 依据此可列式求解.
 B.
B.
 D.
D.


 、
、 、
、 、
、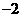 中,最小的实数是( ).
中,最小的实数是( ).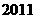 的倒数是( ).
的倒数是( ). 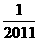 B.
B. D.
D.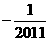
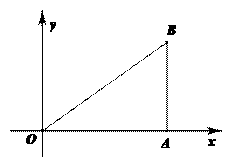 (本题满分10分)如图,已知O(0,0)、A(4,0)、B(4,3).动点P从O点出发,以每秒3个单位的速度,沿△OAB的边0A、AB、B0作匀速运动;动直线l从AB位置出发,以每秒1个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.
(本题满分10分)如图,已知O(0,0)、A(4,0)、B(4,3).动点P从O点出发,以每秒3个单位的速度,沿△OAB的边0A、AB、B0作匀速运动;动直线l从AB位置出发,以每秒1个单位的速度向x轴负方向作匀速平移运动.若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动.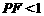
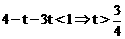
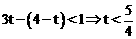
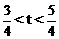 .
.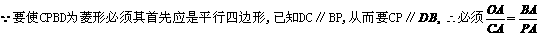
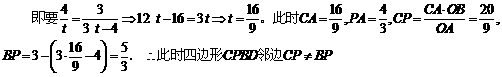
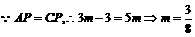 由
由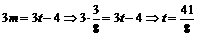
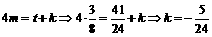
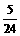 秒,四边形CPBD会是菱形.
秒,四边形CPBD会是菱形.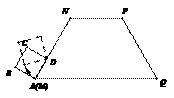 (本题满分6分)如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
(本题满分6分)如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动. ,交MN于
,交MN于 ; ②以DN的中点E(ED=1)为圆心, EA=
; ②以DN的中点E(ED=1)为圆心, EA=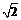 为半径画弧
为半径画弧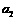 ,
, ;③以N为圆心,NE =1为半径画弧
;③以N为圆心,NE =1为半径画弧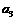 ,
,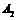 ,
,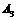 ;④以P为圆心,
;④以P为圆心,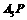 =1为半径画弧
=1为半径画弧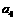 ;⑤在PQ上取F使PF=AD=1,以F为圆心,
;⑤在PQ上取F使PF=AD=1,以F为圆心,
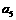 ,
,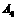 ;⑥在PQ上取G使FG=AD=1,以G为圆心, 1为半径画弧
;⑥在PQ上取G使FG=AD=1,以G为圆心, 1为半径画弧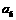 ,
,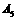 ,交PQ于
,交PQ于 。
。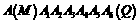 。(画图过程略)
。(画图过程略) 
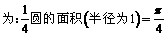 ;
;

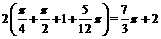
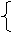 [答案]解:(1) 由图像知
[答案]解:(1) 由图像知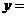
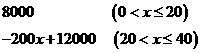
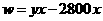
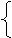 ∴由(1) 有
∴由(1) 有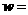
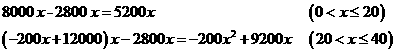
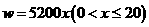 是一次函数一段,最大值5200×20=104000
是一次函数一段,最大值5200×20=104000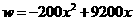
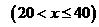 是二次函数一段,当
是二次函数一段,当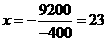 时,
时, 有
有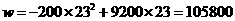 。
。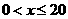 时,函数值为8000得
时,函数值为8000得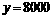 ;
;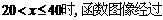
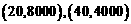 ,由待定系数法可求得
,由待定系数法可求得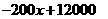 .
.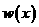 的关系式,分析一次函数和二次函数的最大值可解.
的关系式,分析一次函数和二次函数的最大值可解.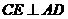 于
于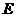 .
.
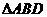 中,
中,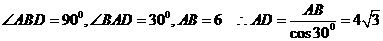
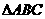 中,
中,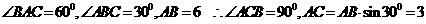
 中,
中,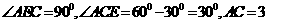
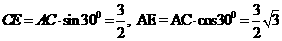
 中,
中,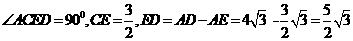
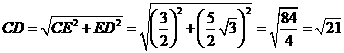
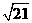 千米
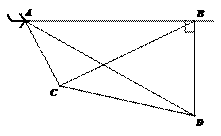
千米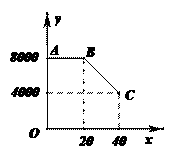 [分析]要求CD的值就要把它放到-个直角三角形中,考虑作
[分析]要求CD的值就要把它放到-个直角三角形中,考虑作 ,
,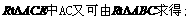 而ED可由AD-AE求得,AE同样可由
而ED可由AD-AE求得,AE同样可由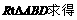 .
.