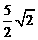0 49550 49558 49564 49568 49574 49576 49580 49586 49588 49594 49600 49604 49606 49610 49616 49618 49624 49628 49630 49634 49636 49640 49642 49644 49645 49646 49648 49649 49650 49652 49654 49658 49660 49664 49666 49670 49676 49678 49684 49688 49690 49694 49700 49706 49708 49714 49718 49720 49726 49730 49736 49744 447348
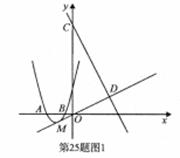
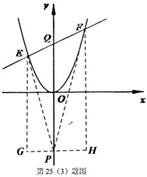
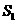 ,是四边形OACD 面积
,是四边形OACD 面积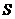 的
的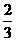 ?若存在,求点 E 的坐标;若不存在,请说明理由.
?若存在,求点 E 的坐标;若不存在,请说明理由.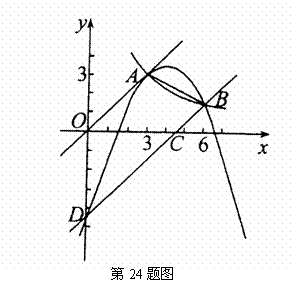

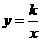 ,把
,把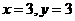 代人解析式中求得
代人解析式中求得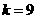 .当
.当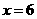 时,
时,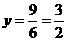 ,所以
,所以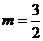 ;
;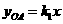 ,把
,把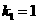 ,则有
,则有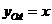 ,
,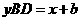 ,把
,把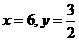 代人解析式中求得
代人解析式中求得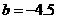 ,则有
,则有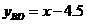 ,所以B(6,1.5)、D(0,-4.5)
,所以B(6,1.5)、D(0,-4.5)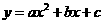 由题意知
由题意知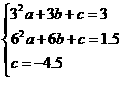 解得
解得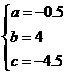
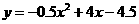
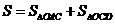 =
=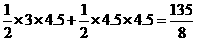 ,
,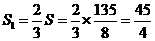
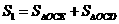
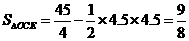 所以
所以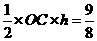 ,求出
,求出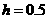 即点E的纵坐标是
即点E的纵坐标是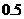 ,把
,把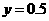 代人
代人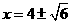 ,所以E(
,所以E(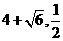 )或E(
)或E(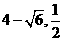 ).
).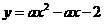 经过点B。
经过点B。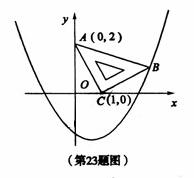
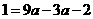 解得
解得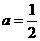 ,所以抛物线的解析式为
,所以抛物线的解析式为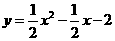
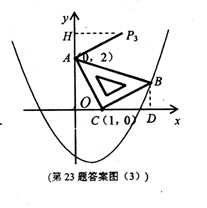
 的图象经过A(
的图象经过A(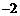 ,
,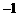 ),B(0,7)两点.
),B(0,7)两点.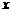 为何值时,
为何值时,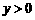 ?
?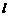 ,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作
,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作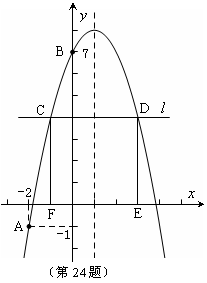

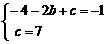 解得
解得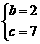
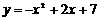 ,
,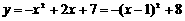 ,所以对称轴为直线
,所以对称轴为直线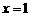 .
.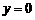 时,
时,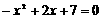 的解为
的解为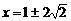 ,
,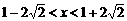 时,
时,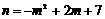 ,即
,即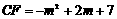
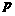 ,则
,则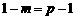 ,所以
,所以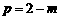 ,所以CD=
,所以CD=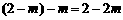
 ,整理,得
,整理,得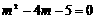 ,解得
,解得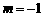 或5.
或5. 只能取
只能取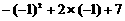 =4
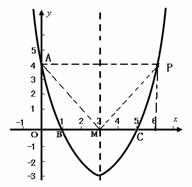
=4 中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴
中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴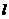 与
与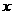 轴相交于点M.
轴相交于点M.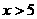 )上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标; (2分)
)上的一点,若以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标; (2分)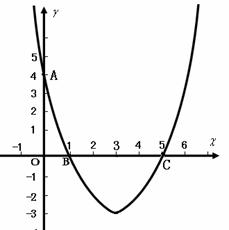
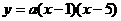 ,
,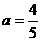 ,
,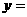
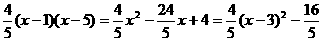 ,
,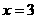 .
.
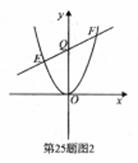
 ,因为抛物线对称轴过点M,所以在抛物线
,因为抛物线对称轴过点M,所以在抛物线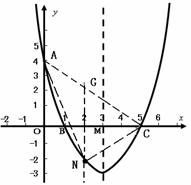
 ,此时点N
,此时点N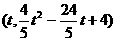 (
( ,过点N作NG∥
,过点N作NG∥ 轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为:
轴交AC于G;由点A(0,4)和点C(5,0)可求出直线AC的解析式为: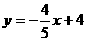 ;把
;把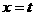 代入得:
代入得: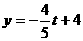 ,则G
,则G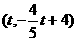 ,
,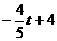 -(
-(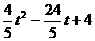 ),
),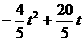 .
.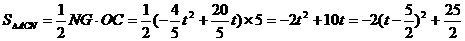
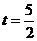 时,△CAN面积的最大值为
时,△CAN面积的最大值为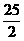 ,
,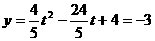 ,∴N(
,∴N(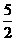 , -3).
, -3).
 =m
=m
 x+b
x+b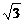 x+b
x+b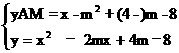
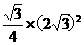 =3
=3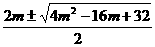 =m
=m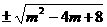
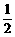 x
x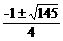 .
. 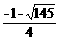 ≤h<
≤h<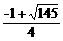 时,平移的抛物线与射线CD只有一个公共点.
时,平移的抛物线与射线CD只有一个公共点.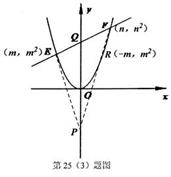
 设EF的解析式为y=kx+3(k≠0).
设EF的解析式为y=kx+3(k≠0).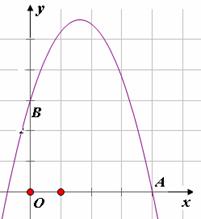
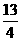 ,
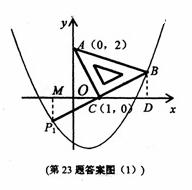
,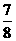 ,0),使得△PAB是以AB为底的等腰三角形.理由如下:
,0),使得△PAB是以AB为底的等腰三角形.理由如下: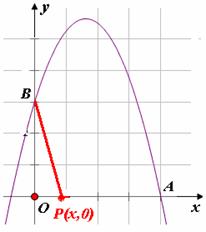
 AE时,如图①,(-1+m)-(-1-m)=
AE时,如图①,(-1+m)-(-1-m)=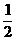
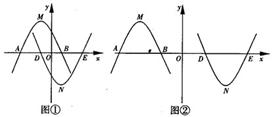
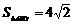 ,求a的值.
,求a的值.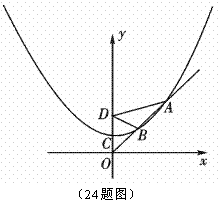

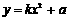
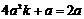
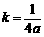
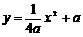
 中,由勾股定理得:
中,由勾股定理得: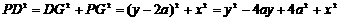

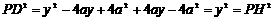
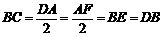
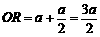 ,
,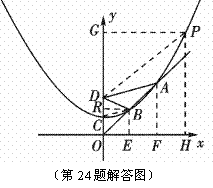 ∴B点的纵坐标是
∴B点的纵坐标是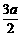 ,又点B在抛物线上
,又点B在抛物线上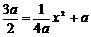 ∴
∴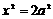
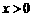 ∴
∴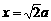 ∴B(
∴B(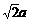 ,
,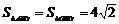
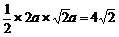
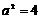 , ∵
, ∵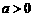 ∴
∴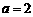
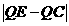 最大?并求出最大值。
最大?并求出最大值。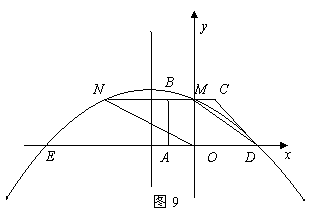

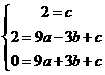
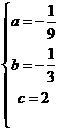
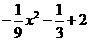
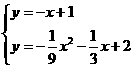
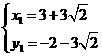
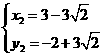
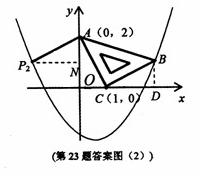
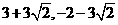 )P2(
)P2(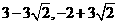 )
)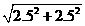 =
=