0 49461 49469 49475 49479 49485 49487 49491 49497 49499 49505 49511 49515 49517 49521 49527 49529 49535 49539 49541 49545 49547 49551 49553 49555 49556 49557 49559 49560 49561 49563 49565 49569 49571 49575 49577 49581 49587 49589 49595 49599 49601 49605 49611 49617 49619 49625 49629 49631 49637 49641 49647 49655 447348
 、
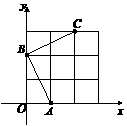
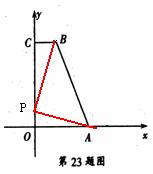
、 均在边长为1的正方形网格格点上.
均在边长为1的正方形网格格点上.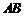 所在直线的函数解析式,并写出当
所在直线的函数解析式,并写出当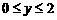 时,自变量
时,自变量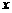 的取值范围;
的取值范围;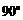 ,得到线段
,得到线段 ,请在答题卡
,请在答题卡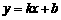 ,
, 随
随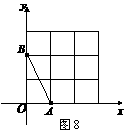

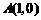 ,
,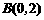
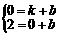
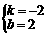
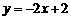
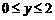 时,自变量
时,自变量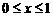 .
.

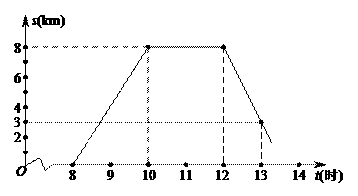
 ,
,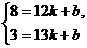 解得:
解得: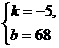
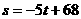 ,
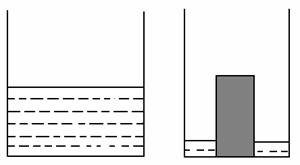
,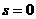 时,t=13.6 ,
时,t=13.6 ,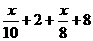 <14, 解得:x<
<14, 解得:x<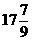 ,
,

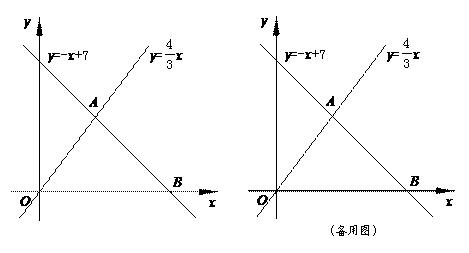


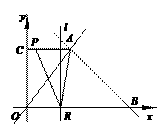
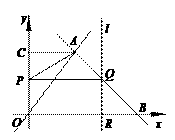
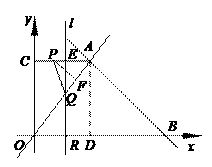
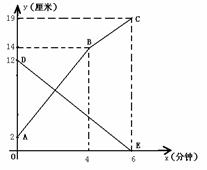
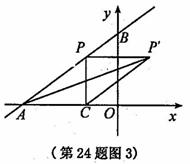
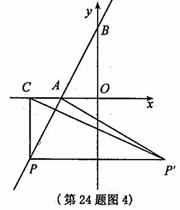
 分别作
分别作 轴,
轴, 轴的垂线,与坐标轴围成矩形
轴的垂线,与坐标轴围成矩形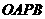 的周长与面积相等,则点
的周长与面积相等,则点
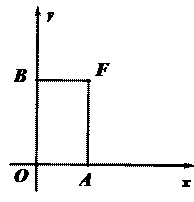
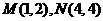 是否为和谐点,并说明理由;
是否为和谐点,并说明理由;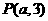 在直线
在直线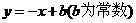 上,求点
上,求点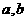 的值.
的值. 
 点
点 不是和谐点,点
不是和谐点,点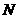 是和谐点.
是和谐点.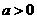 时,
时,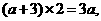
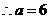 ,点
,点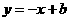 上,代入得
上,代入得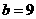 ;
;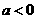 时,
时,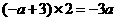
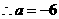 ,点
,点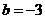 .
.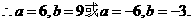
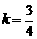 ,
,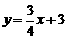
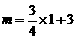 ,∴
,∴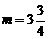 .
.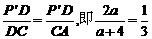 ,
,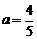 .
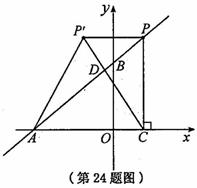
. AC,
AC,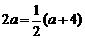 ,∴
,∴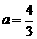 .
.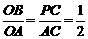 ,即
,即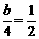 ,
,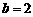 .
.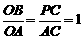 ,即
,即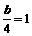 ,∴
,∴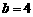 .
.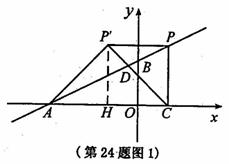
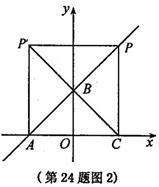
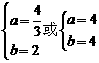 .
.
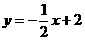 ;②
;②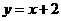 ;③
;③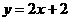 ;④
;④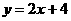 和点C(0,3).则直线
和 是点C的直角线(填序号即可);
和点C(0,3).则直线
和 是点C的直角线(填序号即可);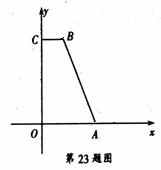
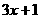 , l2为:y2=
, l2为:y2=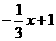 ;
;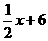 , l2为:y2=
, l2为:y2=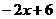 ;
;
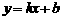 的图象经过M(0,2),(1,3)两点.
的图象经过M(0,2),(1,3)两点.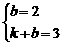 ,解得
,解得 ,∴k,b的值分别是1和2.
,∴k,b的值分别是1和2.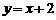 ,∴当y=0时,x=-2,即a=-2.
,∴当y=0时,x=-2,即a=-2.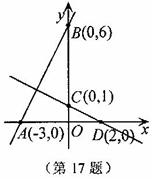
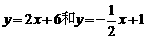 ,解方程组
,解方程组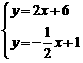 得:
得: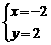 ,则直线AB与直线CD的交点坐标为
,则直线AB与直线CD的交点坐标为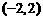 .
.