摘要： 如图.已知二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0).与y轴交于点B. (1)求此二次函数关系式和点B的坐标, (2)在x轴的正半轴上是否存在点P.使得△PAB是以AB为底的等腰三角形?若存在.求出点P的坐标,若不存在.请说明理由. [答案]解:(1)∵二次函数y= -x2+bx+3的图象与x轴的一个交点为A(4,0). ∴0= -42+4b+3. 解得b=. ∴此二次函数关系式为:y= -x2+x+3. 点B的坐标为B(0,3). (2)在x轴的正半轴上是否存在点P(,0).使得△PAB是以AB为底的等腰三角形.理由如下: 设点P(x.0).x＞0.则根据下图和已知条件可得 x2+ 32=(4- x)2. 解得x=. ∴点P的坐标为P(,0). 即.在x轴的正半轴上是否存在点P(,0).使得△PAB是以AB为底的等腰三角形.
网址：http://m.1010jiajiao.com/timu3_id_496474[举报]
如图，已知二次函数y=
x2+bx+c的图象与x轴只有一个公共点M，与y轴的交点为A，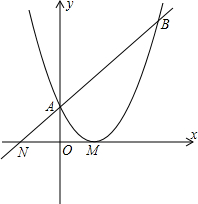
过点A的直线y=x+c与x轴交于点N，与这个二次函数的图象交于点B．
（1）求点A、B的坐标（用含b、c的式子表示）；
（2）当S△BMN=4S△AMN时，求二次函数的解析式；
（3）在（2）的条件下，设点P为x轴上的一个动点，那么是否存在这样的点P，使得以P、A、M为顶点的三角形为等腰三角形？若存在，请写出符合条件的所有点P的坐标；若不存在，请说明理由． 查看习题详情和答案>>
| 1 | 2 |
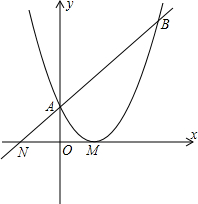过点A的直线y=x+c与x轴交于点N，与这个二次函数的图象交于点B．（1）求点A、B的坐标（用含b、c的式子表示）；
（2）当S△BMN=4S△AMN时，求二次函数的解析式；
（3）在（2）的条件下，设点P为x轴上的一个动点，那么是否存在这样的点P，使得以P、A、M为顶点的三角形为等腰三角形？若存在，请写出符合条件的所有点P的坐标；若不存在，请说明理由． 查看习题详情和答案>>
如图，已知二次函数y=ax2+bx+c的图象过（-1，0）和（0，-1）两点，则化简代数式
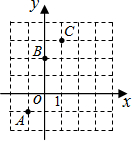如图，已知二次函数y=ax2+bx+c的图象经过A（-1，-1）、B（0，2）、C（1，3）；
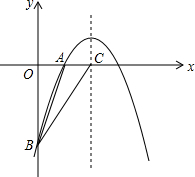（2012•衡水一模）如图，已知二次函数